実数直線の標準位相

標準位相とは、実数全体 \( \mathbb{R} \) において、a < b を満たす開区間 \( (a, b) \) およびそれらの有限または無限の和集合を開集合とする定義に基づく位相のことである。

つまり、集合 U が開集合であるとは、U の中の任意の点 x に対して、x を含む開区間 \( (a, b) \) が存在し、その区間が完全に U に含まれていることを意味する。

$$ x \in (a,b) \subseteq U $$

言い換えれば、開集合 U のすべての点 x は、U に内包される開区間 \( (a, b) \) の中にある。

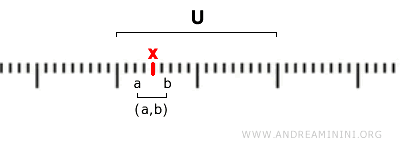
この定義に基づくと、標準位相では次のような集合が開集合として扱われる。

• 開区間
  実数直線 \( \mathbb{R} \) 上の標準位相における開集合は、a < b を満たす開区間 \( (a, b) \) であり、それらの有限または無限の和集合も開集合とみなされる。
• 集合の演算
  開集合には、和集合や有限個の交わりも含まれる。
  • 和集合: 任意個の開集合の和集合は、常に開集合である。
  • 有限交わり: 有限個の開集合の交わりも、やはり開集合である。

標準位相は、実数直線 \( \mathbb{R} \) 上で定義できる多くの位相の中でも最も基本的なものの一つであり、広く使われている。距離や開性、連続性といった直感的な概念を自然に表現できるため、数学の多くの分野で標準的な基盤として採用されている。

注記: 実数直線 \( \mathbb{R} \) やその他の集合上には、異なる基底をもつ別の位相を定義することもできる。その場合、開集合の性質や構造は標準位相とは異なるものとなる。こうした位相は、特定の性質を分析したり、新しい数学的現象を探求する際に利用される。

具体例

実数直線 \( \mathbb{R} \) における標準位相の基底は、a < b を満たすすべての開区間 \( (a, b) \) の集合として定義される。

$$ B = \{ (a,b) \subset; R \ | \ a \lt b \} $$

この位相の重要な特徴は、任意の点 x に対して、x を中心とする小さな開区間が常に存在し、その区間が元の集合 U の中に完全に含まれるという点である。これによって、標準位相における開集合の条件が満たされる。

$$ \forall \ x \ \in U \ \exists \ \epsilon>0 \ | \ x \in (x-\epsilon, x+\epsilon) \subseteq U $$

ここで U は実数直線 \( \mathbb{R} \) 上の標準位相における開集合である。

この位相が「標準位相」と呼ばれるのは、実数直線上で最も基本的かつ広く用いられているからである。

例 2

端点 0 と 1 を含まない開区間 \( (0,1) \) に標準位相を適用してみよう。

この集合が位相空間を構成するかどうかを考える。

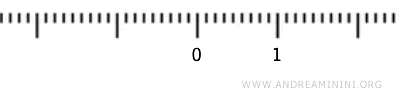
部分集合 \( U \subset (0,1) \) が開集合であるとは、任意の点 \( x \in U \) に対して、実数直線 \( \mathbb{R} \) 上の開区間 \( (a,b) \) が存在し、\( x \in (a,b) \) かつ \( (a,b) \cap (0,1) \subseteq U \) であることを指す。

区間 \( (0,1) \) 自体は、実数直線上の標準位相における開集合の交わりとして表されるため、この条件を満たしている。

したがって、区間 \( (0,1) \) は、実数直線 \( \mathbb{R} \) の標準位相によって誘導される位相をもつ位相空間である。

たとえば、\( (0.1, 0.5) \)、\( (0.2, 0.9) \)、またはその和集合 \( (0.1, 0.5) \cup (0.6, 0.8) \) はいずれも \( (0,1) \) の誘導位相における開集合である。つまり、\( (0,1) \) 内の開集合とは、実数直線上の開集合を \( (0,1) \) に制限したものといえる。

このように、\( (0,1) \) は標準位相の下での \( \mathbb{R} \) の部分空間として、位相空間の基本的な性質をそのまま保持している。

例 3

3 つの整数からなる有限集合 \( X = \{1,2,3\} \) を考えてみよう。

この集合が実数直線 \( \mathbb{R} \) の標準位相のもとで位相空間となるかどうかを調べる。

この場合、集合 X の各要素は開集合にはならない。なぜなら、標準位相の基底は開区間に基づいており、この定義を有限集合に直接適用することはできないからである。

たとえば、X の要素 {2} を実数とみなすと、それは開区間 (2-ε, 2+ε) の中に含まれるが、この区間のほとんどの点は X に属さない。したがって、実数直線 \( \mathbb{R} \) の標準位相における開集合の条件を満たさない。

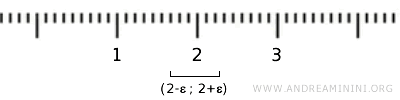
ただし、\( X \) を \( \mathbb{R} \) の部分集合とみなし、「誘導位相（部分空間位相）」を用いれば、開集合は空集合と X 自身のみとなる。この場合、位相的には単純で、あまり興味深い構造ではない。

有限集合のような \( X \) に対しては、すべての部分集合を開集合とみなす離散位相を採用するのが一般的である。

（続く）