位相幾何学（Topology）

位相幾何学（Topology）は、引き伸ばしや曲げ、ねじりといった連続的な変形を加えても変わらない空間の性質を研究する数学の分野である。重要なのは、その過程で対象を切断したり、別々の部分を貼り合わせたりしないという点である。

つまり位相幾何学が注目するのは、変換が連続である限り常に保たれる幾何学的な性質である。

これらの性質が変化するのは、空間の一部を引き裂いたり、二つの部分を接合したりするなど、不連続な操作が行われた場合に限られる。

例えば、球と立方体は位相的に同値である。どちらも、切断や接合を行うことなく、連続的な変形によって互いに移り変わることができるからである。

一方で、球とトーラスは位相的に同値ではない。球をトーラスに変形するには穴を新たに作る必要があり、逆にトーラスを球に戻すには穴を消さなければならない。いずれの場合も、切断や接合を避けることはできない。

このように、位相幾何学は距離や大きさ、形状といった数値的な測定には関心を持たず、空間がどのように構成され、どのようにつながっているかという構造そのものを重視する。

位相的な視点では、長さ、面積、体積、角度といった概念は本質的ではない。重要なのは、図形や空間が持つ質的な特徴と、それらが連続変形によって互いに変換可能かどうかである。

この考え方には、例えば 連結性、コンパクト性、対象が持つ穴の数など、空間全体に関わる性質が含まれる。

位相幾何学では、位相空間という基本概念が導入され、中心的な役割を果たす変換として同相写像が定義される。同相写像とは、連続で全単射であり、さらに逆写像も連続である写像のことで、空間の位相構造を保ったまま変形を記述する。

こうした特徴から、位相幾何学はしばしば「ゴム板幾何学」と呼ばれる。対象は弾性のある素材でできていると想定され、引き伸ばしたり、曲げたり、圧縮したりすることはできるが、切り裂いたり貼り合わせたりすることはできない。位相幾何学は、現代数学において極めて重要であり、さまざまな分野を結びつける基盤となる理論である。

トポロジーの始まり

トポロジーの物語は18世紀、数学者レオンハルト・オイラーのケーニヒスベルクの七つの橋の問題から始まります。

当時、オイラーは「街の七つの橋を一度ずつすべて渡るルートはあるか？」という素朴な問いを考えました。この問題は、長さや距離ではなく「どの地点がどの橋でつながっているか」という構造に関わるものでした。

七つの橋の問題
ケーニヒスベルクの街を流れる川に七つの橋が架かっていました。出発点をどこに選んでも、同じ橋を二度通らずに全ての橋を一度ずつ渡るルートを見つけられるでしょうか？

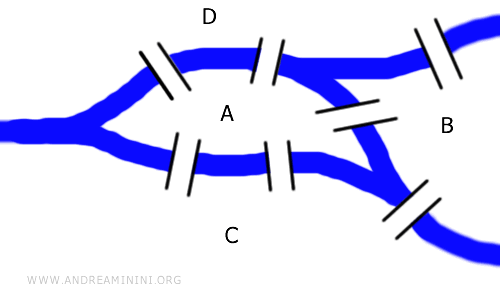
この課題には距離の概念は関係ありません。重要なのは「橋と陸地のつながり方」だけです。したがって、この問題はグラフとして表せます。下の図は、橋の配置を単純化したグラフ表現です。

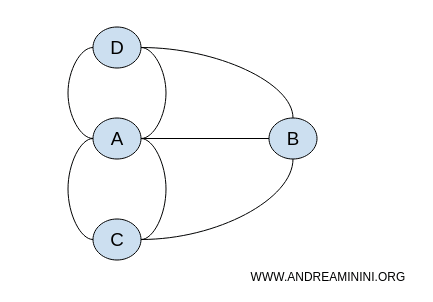
節点（点）の位置はどうでもよく、大切なのはどの点がどの線でつながっているかという関係です。したがって、形は違っても同じ構造をもつグラフはすべて「位相的に等価」と言えます。

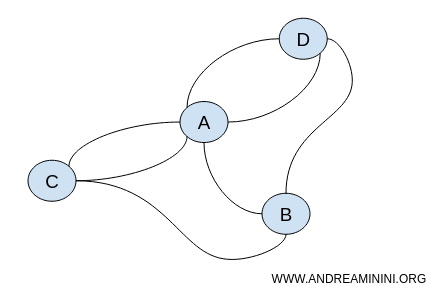
オイラーは、この問題が「測ること」ではなく「つながり方」に関するものであると気づき、解が存在しないことを証明しました。これが「位置の幾何学（geometry of position）」、つまりトポロジーの始まりでした。

その後、ガウス、メビウス、リーマン、クラインといった数学者たちが形や曲面の研究を進め、トポロジーの基礎を築き上げました。19世紀後半には、アンリ・ポアンカレが「代数的トポロジー」を発展させ、現代トポロジーの礎を固めました。

豆知識：ヨハン・リスティングが1847年に初めて「トポロジー」という言葉を使いましたが、この概念が広く受け入れられるまでには数十年かかりました。

形をどう見るか--位相空間の考え方

位相空間とは、ある集合 X に「開集合」と呼ばれる構造を与え、連続性や近さといった概念を抽象的に定義できるようにしたものです。

$$ (X,T) $$

例：実数直線 \( \mathbb{R} \) は、もっとも身近な位相空間の一つです。標準的な位相では、各点の周りに小さな区間を含む集合を開集合と呼びます。これによって「連続な関数」や「極限」といった概念を一般的な形で考えることができます。

形が変わっても同じ？--同相写像

同相写像とは、連続的に変形できる関係を指します。ある空間を別の空間にゆっくり変形していくとき、切ったり貼ったりせずに対応を保てるなら、二つの空間は「同相」、つまりトポロジー的に同じ構造をもっていると言えます。

例：コーヒーカップとドーナツは、形は違ってもどちらも「穴が一つ」あります。切ったり接着したりせずに連続的に変形すれば、片方をもう片方に変えられます。これはまさに同相写像の例です。

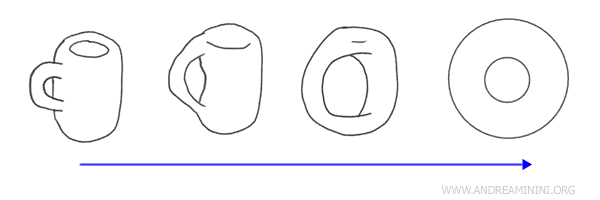
幾何学とのちがい

トポロジーと幾何学は、どちらも「形」を扱いますが、見ているものが違います。

• 幾何学は、距離や角度など「測ること」が中心です。たとえば、図形の回転や対称性は、長さを変えない幾何学的変換です。
  

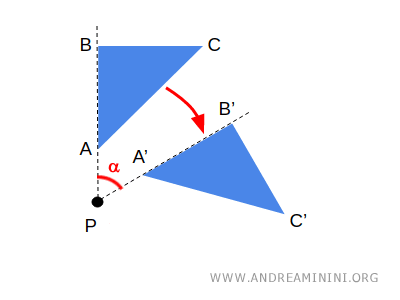
  ユークリッド幾何学では、平行線の性質を定める「第五公準（平行線公準）」が基本ですが、非ユークリッド幾何学ではそれをゆるめ、新しい空間の可能性を探ります。

• トポロジーは、「切らずに変える」変形の中で保たれる性質を研究します。連続性や連結性、形の柔軟さなど、質的な面に注目します。
  

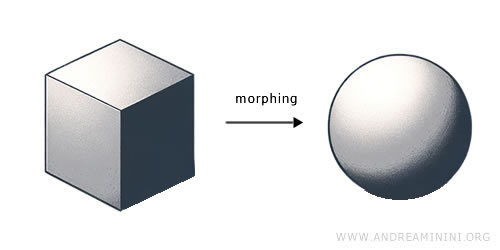
  例：粘土の立方体を押しつぶして球にすることができます。このとき、素材を切り取ったり足したりせずに形を変えられるなら、それは同相写像の一種です。
  

幾何学が「形を測る」学問なら、トポロジーは「形のつながりを理解する」学問だと言えるでしょう。

トポロジーの主な分野

トポロジーは非常に広い分野で、現代数学や科学のさまざまな領域に応用されています。主な分野を挙げると次の通りです。

• 幾何学的トポロジー：切ったり貼ったりせずに行う変形で保たれる性質を研究します。距離ではなく、連続性や境界、コンパクト性などに注目します。
• 一般位相（点集合位相）：もっとも抽象的な分野で、開集合や閉集合、連続性、連結性などを体系的に扱います。
• 代数的トポロジー：代数の考え方を用いて空間を研究し、複雑な形を群や環などの代数構造で表現します。
• 微分トポロジー：微分法を使って、局所的にユークリッド空間のような構造をもつ空間を研究します。滑らかさや接ベクトルなどを扱います。
• 応用トポロジー：データ解析やネットワーク、工学、生物学など、現実の問題にトポロジーの考え方を応用する分野です。

このようにトポロジーは、抽象的でありながらも、世界のさまざまな現象を理解するための強力な道具として広がり続けています。