ハウスドルフ空間とは何か

ハウスドルフ空間は、位相空間の中でも特に扱いやすい構造をもつ空間です。互いに異なる二つの点を、重ならない二つの開近傍で分離できるという性質を持っています。この分離性により、点同士の位置関係を明確に理解できるようになります。

もう少し平易に言うと、ハウスドルフ空間では、どんな二点を選んでも、それらを包み込む二つの開集合を用意でき、それらは必ず重なりません。数学的には \( U \cap V = \emptyset \) と書きます。

この性質は、ユークリッド空間で「点同士はきちんと離れている」という私たちの直感とよく合っています。そのため、解析学や幾何学でも基盤となる重要な概念です。特に、収束する列の極限が一意に決まるなど、議論を進める上での大きな利点があります。

また、ハウスドルフ空間では単一点集合が常に閉集合になるという特徴もあります。裏を返せば、一点を除いた集合は必ず開集合になります。

具体例で理解する

例 1: 実数直線と標準位相

実数直線 \(\mathbb{R}\) に通常与えられる標準位相を考えます。

標準位相では、単一点集合 \( \{x\} \) は開集合ではありません。開集合はそれぞれの点の周りに必ず開区間を含む必要があるため、単一点ではその条件を満たさないからです。

一方、補集合 \( \mathbb{R} \setminus \{x\} \) は開集合です。

このため、単一点集合は閉集合となります。

さらに実数直線はハウスドルフ空間です。異なる二点 \( a \) と \( b \) を取ると、それぞれのまわりに重ならない開区間を簡単に選ぶことができます。

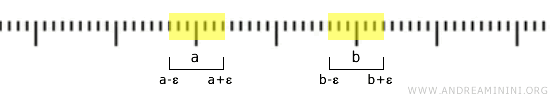
例えば \( a < b \) の場合、十分小さな \( \varepsilon \) を取れば、区間 \( (a-\varepsilon, a+\varepsilon) \) と \( (b-\varepsilon, b+\varepsilon) \) は互いに重なりません。

このように、標準位相がハウスドルフであることは、直感的にも納得しやすい構造です。

例 2: 離散位相をもつ集合

次に、集合 \( X = \{1, 2, 3\} \) に離散位相を与えた場合を考えます。

離散位相では、X のすべての部分集合が開集合です。これは極めてシンプルで扱いやすい位相です。

したがって、空集合から全体集合まで、全部で \(2^3 = 8\) 個の開集合があります。

離散位相空間は必ずハウスドルフ空間になります。異なる二点 \( x \) と \( y \) に対して、それぞれを含む単一点集合 \( \{x\} \) と \( \{y\} \) を近傍として選べば、これらは自動的に重なりません。

例えば

$$ \{1\} \cap \{2\} = \emptyset $$

となり、ハウスドルフ性が明確に確認できます。

標準位相と離散位相の根本的な違いは、標準位相では開集合に一定の条件があり、すべての部分集合が開になるわけではないという点です。この違いが位相空間の性質に大きく影響します。

ハウスドルフ空間が重要である理由

ハウスドルフ空間の最も重要な性質の一つは、収束する列の極限が必ず一意に定まるという点です。

異なる二点に同時に収束する列は存在しません。なぜなら、それら二点の開近傍が必ず重なってしまい、ハウスドルフの分離条件に反するからです。

証明の概要: 列 \( x_1, x_2, \dots \) が異なる二点 x と y に収束すると仮定すると、それぞれの近傍に入るはずの項が必ず重なる時点が現れます。その結果、
$$ A \cap B \neq \emptyset $$ となり、ハウスドルフ空間の定義に反します。よって極限は一意です。

この性質は、解析学の多くの議論で不可欠です。極限があいまいだと、関数や列の振る舞いを正しく扱うことができないからです。

以上が、ハウスドルフ空間の要点と、その理解に役立つ具体例です。