位相空間における単連結空間とは

単連結（simply connected）な位相空間とは、空間の中にあるどんな閉曲線（閉じた経路）も、空間の外に出ることなく連続的に一点へと縮められる空間のことを指す。

もう少し直感的に言えば、どんなループを描いても、それを切ったり持ち上げたりすることなく、ゆっくりと一点に縮めることができる空間が単連結である。

この性質は、空間が一つのまとまりとして連続しており、内部に「穴」を持たないことを意味している。

注記：単連結な空間は必ず連結でもある。しかし、その逆は必ずしも正しくない。連結であっても単連結でない空間も存在する。

例で考えてみよう

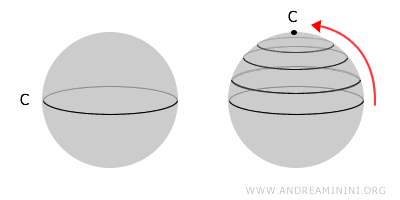
球面を思い浮かべてみよう。球面は典型的な単連結空間である。球面上のどんな閉曲線も、表面を離れることなく連続的に一点に縮めることができる。

対照的に、ドーナツ形のトーラスには中心に穴がある。そのため、穴を回り込むようなループは一点に縮めることができない。したがって、トーラスは単連結ではない。

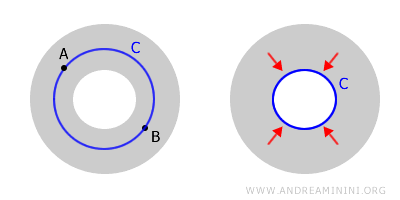
この例から、単連結であることと単に連結であることの違いがよく分かる。ドーナツ形のトーラスは、空間内のどの2点も経路で結ぶことができるため連結ではある。しかし、すべての閉曲線を一点に縮められるわけではないため、単連結ではない。

このように、連結ではあるが単連結でない空間は多重連結空間（multiply connected space）と呼ばれる。代表的な例として、環状領域（リング状の部分）やトーラスがある。

まとめると、単連結性は弧状連結性（arc connectivity）よりも強い条件であり、空間の「つながり方」をより厳密に表す概念といえる。

単連結性を理解することで、空間の形や構造をより深く捉えることができる。それは、数学だけでなく、物理学や工学、さらにはコンピュータグラフィックスなどにも応用される重要な考え方である。