部分位相（Subspace Topology）とは何か

位相空間 $ (X, T) $、つまり集合 $ X $ とその上の開集合族 $ T $ が与えられているとする。ここで $ Y \subseteq X $ を部分集合として取り出すと、$ Y $ 上には自然に部分位相（subspace topology）が定まる。これは次のように定義される。
\[ T_Y = \{\, U \cap Y \mid U \in T \,\} \]
この集合族が $ Y $ の開集合全体を与える。部分位相は誘導位相（induced topology）とも呼ばれ、元の空間の位相構造をそのまま受け継ぐ形になっている。

つまり、$ V \subseteq Y $ が開であるとは、ある開集合 $ U \subseteq X $ を使って $ V = U \cap Y $ と表せる場合に限る。部分空間における開集合は全てこの形に統一される。

$$ V_{open \ in \ Y} = U \cap Y $$

閉集合についても同様で、$ Y $ における閉集合はすべて $ X $ の閉集合 $ C $ と $ Y $ の共通部分として表せる。

$$ V_{closed \ in \ Y} = C \cap Y $$

このように、位相部分空間とは大きな位相空間の部分集合が、その空間から誘導された位相を持つものだと理解できる。

Note. 部分位相空間で開となる集合が、必ずしも元の空間でも開であるとは限らない。逆に、元の空間で閉だが部分位相では開になる場合もある。もちろん、両方で開または両方で閉となる集合も存在し、同時に開であり閉でもある「閉開集合」（clopen）が現れることもある。以下の例でその理由がより明確になる。

具体例で理解する部分位相
部分位相の基本性質
補足

具体例で理解する部分位相

標準位相をもつ実数全体の空間 $ \mathbb{R} $ を考える。ここでは開集合はすべて開区間で記述できる。

この空間から部分集合 $ Y = [0,1] $ を取り出す。

部分位相における開集合は一般に次の形をしている。

$$ U \cap [0,1] $$

ここで $ U $ は $ \mathbb{R} $ の開集合である。

たとえば、開集合 (-1, 0.5) を考える。

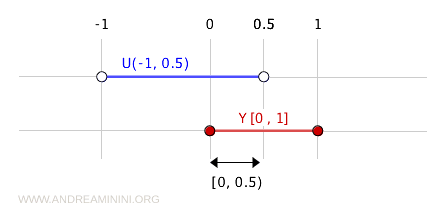
部分位相の例

この集合を部分集合 $ Y=[0,1] $ と交わすと次が得られる。

$$ (-1,0.5) \cap [0,1] = [0,0.5) $$

したがって $ [0,0.5) $ は部分空間 $ Y $ において開となる。ただし標準位相の $ \mathbb{R} $ では開ではない点に注意する必要がある。

同じように、閉区間 $[-1,0.5]$ と $ Y $ の共通部分を取ると、

$$ [-1,0.5] \cap [0,1] = [0,0.5] $$

この区間 $ [0,0.5] $ は部分位相では閉集合となる。

Note. 例えば 0 具体例として、
$$ (-1,0.5) \cap [0,1] = [0,0.5) $$
が挙げられる。

もちろん、部分位相 $ Y $ と元の位相空間 $ X $ の双方で開となる集合もある。たとえば (0.2, 0.8) がその例である。

逆に両方で閉となる集合もあり、[0.2, 0.8] が代表的である。

さらに、部分空間 $ Y=[0,1] $ において集合 $ [0,1] $ は開であり閉でもあるという興味深い性質を持つ。

開である理由
開集合 $ U=\mathbb{R} $ を取れば、
$$ U \cap Y = \mathbb{R} \cap [0,1] = [0,1] $$
となるため、$ [0,1] $ は部分空間 $ Y $ において開となる。
閉である理由
閉集合 $ C=[0,1] $ を用いれば、
$$ C \cap Y = [0,1] $$
と書けるので、$ [0,1] $ は部分空間 $ Y $ において閉集合でもある。
Note: $ Y $ における補集合が空集合になることからも閉集合であることが分かる。空集合は常に開集合であるため、その補集合は閉である。

このように、部分位相空間では元の空間とは異なる開閉性が現れることがあり、その構造は位相空間論の理解を深めるうえで重要な題材となる。

特に、開でもあり閉でもある集合は「閉開集合」（clopen）と呼ばれ、位相の性質を調べる際にしばしば鍵となる。

例 2

実数全体の集合 $\mathbb{R}$ に標準位相を入れて考えてみよう。この位相では、開区間 (a, b) が基本となり、そこから多くの性質が生まれる。

その中でも特に身近な例が、整数全体の集合 $\mathbb{Z}$ を部分空間として取り出した場合である。驚くかもしれないが、$\mathbb{Z}$ の部分位相は離散的な構造をもち、各整数がそのまま開集合として扱える。

例えば整数 7 は次のように得られる。

$$ (6.5, 7.5) \cap \mathbb{Z} = \{ 7 \} $$

同じ方法で任意の整数が取り出せるため、$\mathbb{Z}$ 上では単点集合がすべて開になる。さらにその合併も開集合となるので、任意の部分集合が開集合として扱える。

集合 {6, 7, 8} を見てみると、このように得られる。

$$ (5.5, 8.5) \cap \mathbb{Z} = \{ 6, 7, 8 \} $$

このような理由から、$\mathbb{Z}$ に誘導される部分位相は離散位相と一致する。数学的には非常に扱いやすく、例として頻繁に登場する構造である。

Note: $\mathbb{Z}$ 上の離散位相は独立した位相としても定義できるが、標準位相を持つ $\mathbb{R}$ から誘導される部分位相と一致する。

例 3

次に、三次元空間 $\mathbb{R}^3$ とその標準位相を考えてみる。この空間では、開集合は開球を基本として構成される。

ここから半径 1 の球面、つまり単位球面 $ S^2 $ を取り出してみよう。

$$ S^2 = \{ (x, y, z) \in \mathbb{R}^3 \mid x^2 + y^2 + z^2 = 1 \} $$

$ S^2 $ の部分位相は、$\mathbb{R}^3$ の開集合との共通部分として定義される。これは、部分位相の最も自然な例の一つである。

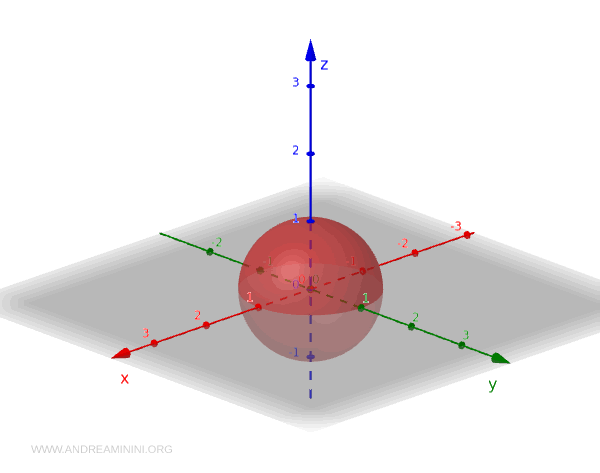
部分空間としての球面

では、球面上の開集合をいくつか見てみよう。

球面全体が開集合になる場合
$ U = \{ (x,y,z) \mid x^2 + y^2 + z^2 < 2 \} $ のような開集合を取ると、球面上のすべての点はこの条件を満たすため、
$$ U \cap S^2 = S^2 $$
となり、球面そのものが部分位相における開集合になる。
上半球のような局所的な領域
$ U = \{ (x,y,z) \mid z > 0 \} $ を使えば、上向きの半球部分が自然に得られる。これは直感的にも理解しやすい開集合の例である。
部分位相の基本性質
空集合と $ S^2 $ 自体は常に開であり、開集合同士の有限交叉や任意合併も開である。これは位相空間の基本法則そのものである。

このように、球面 $ S^2 $ の位相は外側の空間 $\mathbb{R}^3$ から自然に誘導され、開集合の構造も直感的に把握できる。

部分位相の基本性質

部分位相がどのように振る舞うか、その基本をまとめておく。

開集合の形が明確
部分集合 $ Y $ における開集合はすべて $ U \cap Y $ の形で表される。
空集合と全体集合が常に開
空集合 $ \emptyset $ も $ Y $ 自体も例外なく開集合である。
有限交叉が閉じている
$ Y $ の有限個の開集合の交叉は、再び $ Y $ の開集合になる。
任意合併が閉じている
任意個の開集合の合併も $ Y $ の開集合になる。

補足

部分位相を理解する上で役立つ補足事項を挙げる。

$\mathbb{R}^n$ の部分集合 $ Y $ に対して定義される標準位相は、$\mathbb{R}^n$ の部分位相と一致する。直感的で扱いやすい性質である。
例. $ Y = [-1,0) \cup (0,1] $ を例に取ると、次のように開集合として得られる。
$$ (-1.5,0.5) \cap Y = [-1,0) $$ $$ (0,1.5) \cap Y = (0,1] $$ この場合、両方の区間は開であると同時に閉でもあり、閉開集合（clopen）として振る舞う。
部分位相の基底定理
位相空間 $ X $ の基底 $ B_X $ から、部分集合 $ Y $ の部分位相に対する基底が自然に構成できる。
$$ B_Y = \{\, B \cap Y \mid B \in B_X \,\} $$

以上が部分位相を学ぶ際に押さえておきたい核心的な内容である。概念そのものは素朴だが、位相空間論の多くの議論に深く関わる重要な構造となる。