開長方形を基底とする位相

開長方形を基底とする位相とは、平面 R² において、開集合が開長方形の集まりとして表される位相のことです。ここでいう開長方形とは、二つの開区間を組み合わせて作られる領域で、二次元空間の構造を直感的に捉えるのに役立ちます。

この位相では、すべての開長方形近傍が基底として働き、これらの集合を組み合わせることで、より複雑な開集合を形づくります。

具体的には、集合 \( U \subseteq \mathbb{R}^2 \) が開であるとは、任意の点 \( (x, y) \in U \) のまわりに、その点を含み、かつ \( U \) の内部にすっぽり収まる開長方形が一つ見つかることを意味します。

開長方形は、ユークリッド平面の位相を理解するための、扱いやすく見通しのよい基底として機能します。

$$ B= \{ (a, b) \times (c, d) | a< b, c

ここで \( a, b, c, d \) は実数で、\( a< b \) と \( c

この基底は、通常の標準位相（開球や開円板で定義される位相）を別の視点からとらえ直したもので、R² の開集合が多様な方法で記述できることを示しています。

Note: 位相空間の基底は一つに限られません。条件を満たす集合族であれば、円板でも長方形でも、同じ開集合系を作り、同じ位相を生み出します。形が異なっても、位相そのものは変わりません。

開長方形の例

R² における開長方形は、二つの開区間を直積して得られる最も基本的な開集合です。

例えば、\( x \) 軸方向の開区間 \( (1, 3) \) と、\( y \) 軸方向の開区間 \( (2, 4) \) を見てみましょう。

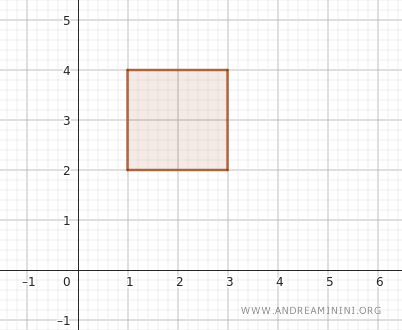
この二つを組み合わせると、\( x \) が 1 と 3 の間にあり、\( y \) が 2 と 4 の間にある全ての点 \( (x, y) \) が含まれる開長方形になります。

この集合は形式的に \( (1, 3) \times (2, 4) \) と書けます。

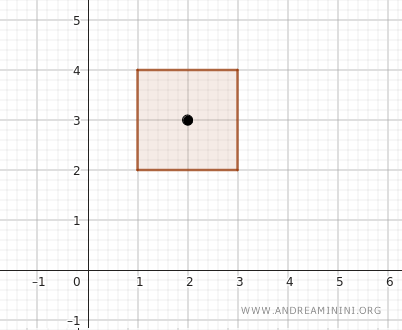
例えば点 \( (2, 3) \) を取ると、\( x \) 座標は 1 と 3 の間、\( y \) 座標は 2 と 4 の間にあり、確かにこの開長方形に含まれます。

Note: 開長方形には境界は含まれません。たとえば \( (1, y) \)、\( (3, y) \)、\( (x, 2) \)、\( (x, 4) \) のような点はすべて外側にあり、開集合の条件を満たしません。