開集合と位相を理解する

要するに、位相 T は X の開集合だけを集めた集合族であり、和集合と共通部分の操作に対して閉じていることが重要となる。

なお、集合族とは、要素が集合そのもので構成された集合のことを指す。

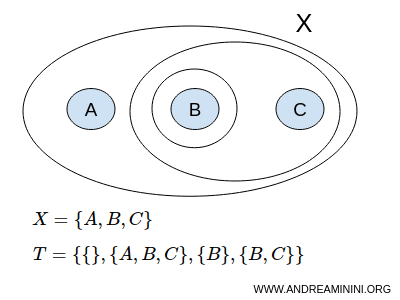
このように、集合 X と位相 T が与えられると、その組 (X, T) を位相空間と呼ぶ。

補足. 一般には「X は位相空間である」と簡単に表現されるが、正確には集合 X と位相 T の組によって初めて位相空間が成立する。

空集合はなぜ開集合なのか

空集合はすべての位相空間で開集合とみなされる。これは位相の定義を矛盾なく成り立たせるために必要なルールであり、位相という体系の基盤となる考え方の一つである。

具体例で考える位相

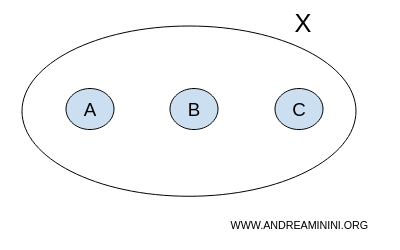
まず、要素 A, B, C を持つ集合 X を考える。

$$ X = \{ A,B,C \} $$

次のような集合族 T を考えてみよう。

$$ T = \{ \{ \},\{A,B,C \}, \{ B \}, \{ B,C \}  \} $$

{ } は空集合、{A,B,C} は集合 X 全体である。定義により、これらは開集合として常に受け入れられる。

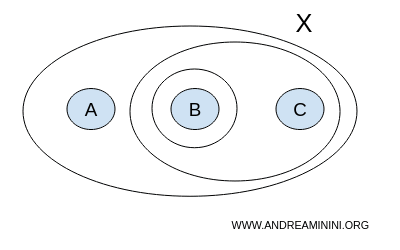
ここで確認しておきたいのは、T に含まれる開集合同士の和集合や共通部分が、常に T に含まれているかどうかである。和集合が閉じていれば

$$ \{ B \} \cup \{ B, C \} \subseteq \{ B, C \} \subseteq T$$

のように、共通部分についても

$$ \{ B \} \cap \{ B, C \} \subseteq \{ B \} \subseteq T$$

と確認できる。すべてのケースでこの性質が成り立つため、T は集合 X の位相と言える。

成立しない例

次に、先ほどと同じ集合 X に対して、次のような集合族を考える。

$$ T = \{ \{ \},\{A,B,C \}, \{ A \}, \{ B \}, \{ B,C \}  \} $$

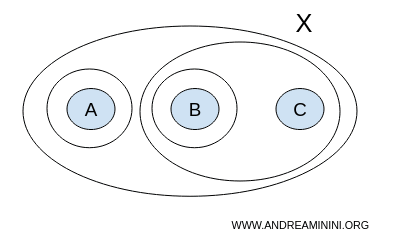
一見すると成立しそうだが、ここでは {A} と {B} の和集合 {A,B} が T に含まれていない。

$$\require{cancel} \{ A \} \cup \{ B \} = \{ A, B \} \cancel{\in} T  $$

つまり、開集合とみなしている集合同士の和集合が T に含まれず、開集合と認められなくなる。この時点で位相の条件に反していることが分かる。

したがって、この T は集合 X 上の位相にはならない。

以上のように、開集合の集まりが位相になるかどうかは、和集合と共通部分の性質によって判断できる。この視点を押さえておくと、より複雑な位相空間を学ぶ際にも役立つ。