集合AとBの内部の和集合
集合 $ A $ と $ B $ の内部の和集合は、常にそれらの和集合の内部に含まれる。すなわち、\[ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B) \] が成り立つ。ただし、等号が必ず成立するとは限らない。
この性質は、2つの集合の内部をそれぞれ取り、その和集合を考えると、それが常に元の2集合の和集合の内部に含まれることを示している。
しかし、この2つの集合が常に等しくなるとは限らない。言い換えると、次の等式は一般には成立しない。
$$ \text{Int}(A) \cup \text{Int}(B) = \text{Int}(A \cup B) $$
包含関係は成立しても、等号が成立しない場合がある。
$$ \text{Int}(A) \cup \text{Int}(B) \ne \text{Int}(A \cup B) $$
この点を区別して理解することは、位相空間における集合とその内部の関係を正確に把握する上で重要である。
具体例
標準的な位相をもつ実数直線 \(\mathbb{R}\) 上の2つの開区間 \( A \) と \( B \) を考える。
$$ A = (0, 2) $$
$$ B = (1, 3) $$
開区間の内部は区間そのものなので、次が成り立つ。
$$ \text{Int}(A) = (0, 2) $$
$$ \text{Int}(B) = (1, 3) $$
内部の和集合は次のようになる。
$$ \text{Int}(A) \cup \text{Int}(B) = (0, 2) \cup (1, 3) $$
この2つの区間の和集合は、最小の点から最大の点までを覆う区間である。
$$ (0, 2) \cup (1, 3) = (0, 3) $$
集合 \( A \) と \( B \) の和集合は次の通りである。
$$ A \cup B = (0, 2) \cup (1, 3) $$
これらの区間は重なっているため、次のように簡単化できる。
$$ A \cup B = (0, 3) $$
和集合 \( A \cup B \) の内部は次のようになる。
$$ \text{Int}(A \cup B) = \text{Int}((0, 3)) = (0, 3) $$
ここで性質を確認する。
$$ \text{Int}(A) \cup \text{Int}(B) = (0, 2) \cup (1, 3) = (0, 3) $$
$$ \text{Int}(A \cup B) = \text{Int}((0, 3)) = (0, 3) $$
この例では、内部の和集合が和集合の内部に含まれていることが明確に分かる。
$$ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B) $$
さらに、この特定の場合には等号も成立している。
$$ \text{Int}(A) \cup \text{Int}(B) = \text{Int}(A \cup B) $$
ただし、他の状況では等号が成立しないこともある。
例えば、次の2つの閉区間を集合として考える。$$ A = [0, 2] $$ $$ B = [2, 3] $$ それぞれの内部は $$ \text{Int}(A) = (0, 2) $$ $$ \text{Int}(B) = (2, 3) $$ である。一方、和集合 $ A \cup B = [0, 3] $ の内部は集合 $ (0, 3) $ となる。$$ \text{Int}(A \cup B) = (0,3) $$ このとき、$ (0, 2) \cup (2, 3) $ は $ (0, 3) $ に含まれるため、包含関係は成立する。$$ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B) $$ しかし、等号は成立しない。なぜなら、点 $ 2 $ は和集合の内部に含まれる。$$ 2 \in \text{Int}(A \cup B) = (0, 3) $$ 一方で、この点は $ \text{Int}(A) $ にも $ \text{Int}(B) $ にも含まれない。$$ 2 \notin \text{Int}(A) $$ $$ 2 \notin \text{Int}(B) $$ したがって、点 $ 2 $ は内部の和集合には含まれない。$$ 2 \notin \text{Int}(A) \cup \text{Int}(B) = (0, 2) \cup (2, 3) $$ このため、2つの集合は等しくない。$$ \text{Int}(A) \cup \text{Int}(B) \ne \text{Int}(A \cup B) $$ この例は、一般に内部の和集合は和集合の内部に含まれるものの、常に等しいとは限らないことを示している。
例2
次に、互いに重ならない2つの開区間を考える。
$$ A = (0, 1) $$
$$ B = (2, 3) $$
いずれも開集合であるため、それぞれの内部は区間そのものである。
$$ \text{Int}(A) = (0, 1) $$
$$ \text{Int}(B) = (2, 3) $$
内部の和集合は次の通りである。
$$ \text{Int}(A) \cup \text{Int}(B) = (0, 1) \cup (2, 3) $$
集合 \( A \) と \( B \) の和集合は次のようになる。
$$ A \cup B = (0, 1) \cup (2, 3) $$
和集合 \( A \cup B \) の内部は次の通りである。
$$ \text{Int}(A \cup B) = \text{Int}((0, 1) \cup (2, 3)) = (0, 1) \cup (2, 3) $$
ここでも性質を確認できる。
$$ \text{Int}(A) \cup \text{Int}(B) = (0, 1) \cup (2, 3) $$
$$ \text{Int}(A \cup B) = \text{Int}((0, 1) \cup (2, 3)) = (0, 1) \cup (2, 3) $$
この場合も、次が成立している。
$$ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B) $$
これらの \(\mathbb{R}\) における基本的な例から、2つの区間の内部の和集合は、それらの和集合の内部に含まれることが確認できる。また、これらの特定の例では等号も成立している。
$$ \text{Int}(A) \cup \text{Int}(B) = \text{Int}(A \cup B) $$
しかし、より複雑な空間では、部分的な重なりによって包含は成立しても、等号が成立しない場合がある。
例3
標準的な位相をもつ実平面 \(\mathbb{R}^2\) における2つの集合 \( A \) と \( B \) を考える。
集合 \( A \) と \( B \) は、それぞれ中心が \( (0, 0) \) と \( (0.5, 0) \)、半径がともに \( 1 \) の、部分的に重なり合う2つの開円板である。
$$ A = \{ (x, y) \in \mathbb{R}^2 \mid x^2 + y^2 < 1 \} $$
$$ B = \{ (x, y) \in \mathbb{R}^2 \mid (x - 0.5)^2 + y^2 < 1 \} $$
このような開集合では、集合の内部は集合そのものに等しい。したがって、次が成り立つ。
$$ \text{Int}(A) = A $$
$$ \text{Int}(B) = B $$
よって、内部の和集合は単に2つの円板の和集合である。
$$ \text{Int}(A) \cup \text{Int}(B) = A \cup B $$
集合 \( A \) と \( B \) の和集合は、2つの円板が部分的に重なった領域である。
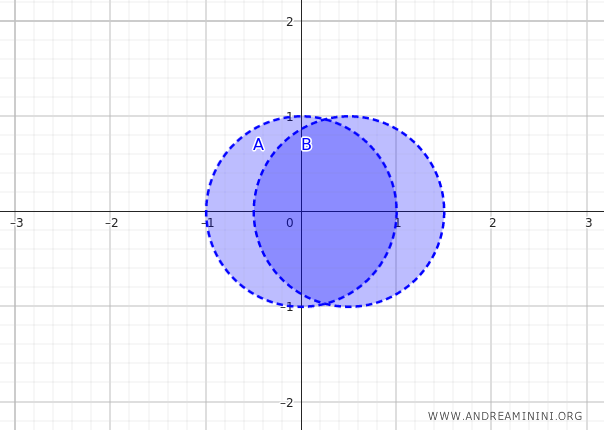
集合 \( A \cup B \) の内部は、その中に完全に含まれる近傍をもつすべての点からなる。
$$ \text{Int}(A \cup B) = A \cup B $$
この例においても、包含関係は成立している。
$$ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B) $$
証明
内部の和集合に関する性質を証明するために、次を示す。
$$ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B) $$
まず、集合の内部の定義を確認する。
集合 \( X \) の内部 \(\text{Int}(X)\) とは、\( X \) の内部点全体からなる集合である。
すなわち、点 \( x \) が \( X \) の内部点であるとは、\( x \) を含み、かつ \( X \) に完全に含まれる近傍が存在することを意味する。
いま、点 \( x \in \text{Int}(A) \cup \text{Int}(B) \) を取る。このとき、\( x \) は \(\text{Int}(A)\) または \(\text{Int}(B)\) のいずれかに属する。
- \( x \in \text{Int}(A) \) であれば、\( x \) を含み、\( A \) に含まれる近傍 \( U_x \) が存在する。
- \( x \in \text{Int}(B) \) であれば、\( x \) を含み、\( B \) に含まれる近傍 \( V_x \) が存在する。
いずれの場合でも、\( x \) の近傍 \( U_x \) または \( V_x \) は \( A \cup B \) に含まれる。
したがって、\( x \) は \( A \cup B \) の内部点である。
以上より、\(\text{Int}(A) \cup \text{Int}(B)\) の任意の点は、\( A \cup B \) の内部点であることが分かる。従って、
$$ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B) $$
これで証明は完了である。