閉集合
位相空間 X の部分集合 B が閉集合であるとは、補集合 X-B の任意の点 u∈X-B に対して、その点を中心とする近傍が常に補集合 X-B に含まれる場合をいう。 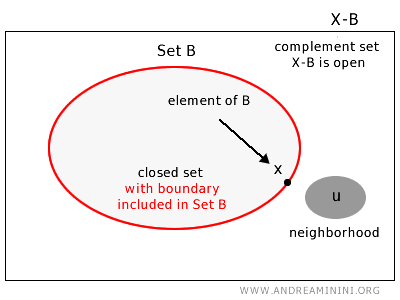
直感的には、閉集合とは境界点をすべて含む集合のことである。
より厳密には、位相空間 X において集合 B が閉集合であるとは、その補集合 X-B が開集合であることを意味する。
注: これは閉集合 B に属する点の中には、自身を完全に含む近傍を持たない点が存在し得ることを示している。
具体例
実数直線 R を考え、閉区間を例として取り上げる。
閉区間とは 実数直線 R における閉区間とは、$ a \lt b $ を満たす実数 a, b に対して、a≤x≤b を満たす全ての実数 x の集合である。
閉区間は [a,b] と表記され、角括弧は端点 a と b が集合に含まれることを示す。
例えば、閉区間 [3,10] は実数直線 R における典型的な閉集合である。
このとき集合 B には 3 から 10 までの無数の実数が含まれる。
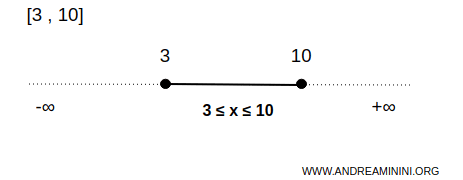
すなわち、3≤x≤10 を満たす全ての点が集合に属し、端点 3 と 10 も含まれる。
しかし、区間 [3,10] に属するすべての点が、区間の内部に完全に収まる近傍を持つわけではない。
例えば端点 x=3 の任意の近傍は、必ず区間 [3,10] の外側の点を含んでしまう。
注: たとえ 3±0.00000001 のような極めて小さな近傍を考えても、3-0.00000001 は 3 より小さいため、その近傍全体は区間 [3,10] に含まれない。同様のことは端点 x=10 にも当てはまる。
これは一次元における閉集合の素朴で分かりやすい例である。
その他の閉集合の例
同じ考え方は二次元にも拡張できる。
例えば、中心 (0,0)、半径 r=1 の円板を考える。
$$ x^2+y^2 \le 1 $$
この不等式は、原点からの距離が 1 以下である全ての点を表し、円周上の点も内部の点も含んでいる。
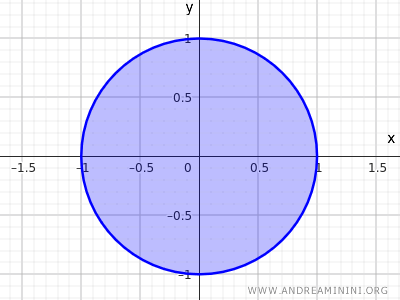
これも閉集合の一例である。
容易に分かるように、円周上の点はそれ自身を完全に含む近傍を持たない。
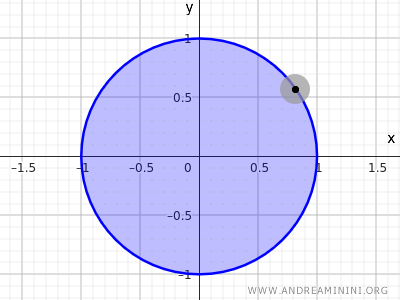
注: 位相空間 R2 において、方程式 $ x^2+y^2=1 $ が表す円周は内部を含まないため開集合でも閉集合でもない。これに対し、不等式 $ x^2+y^2 \le 1 $ が表す集合は境界を含むため閉集合である。
この考え方は三次元の球面や n 次元空間の球にも自然に一般化される。
閉集合の補集合
空間 X において、閉集合 C の補集合 X-C は開集合となる。
C が X における閉集合ならば、その補集合 X-C は必ず開集合である。
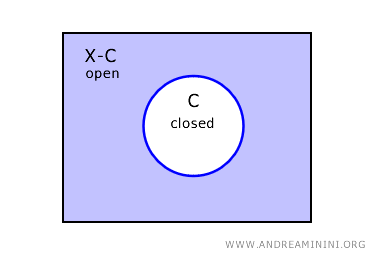
逆に、集合 U が開集合であるならば、その補集合 X-U は閉集合となる。
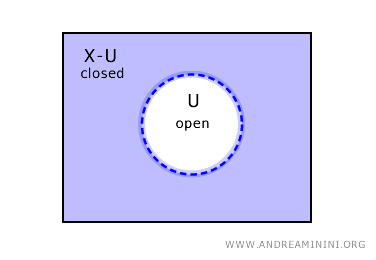
ただし、位相空間にはこの二分類だけではなく、開かつ閉である集合や、開でも閉でもない集合が存在する場合もある。
つまり「閉でない」ことは「開である」ことを意味せず、「開でない」ことも「閉である」ことを意味しない。
例
集合 X={a,b,c,d} に位相 T を導入した場合を考える。
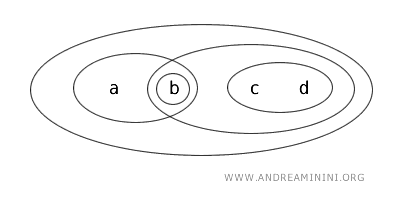
この位相 T において、次の集合が開集合として定義されている: {b}, {a,b}, {c,d}, {b,c,d}, {a,b,c,d}, Ø。
それぞれの性質を確認する。
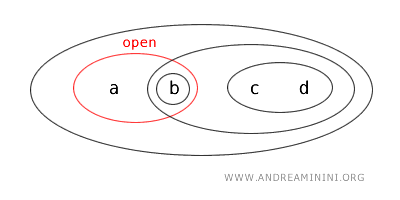
- {b} は開集合である。これは位相 T により明示的に開として定められている。
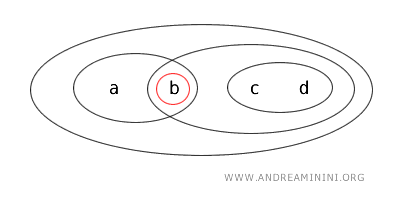
- {a} は閉集合である。X-{b,c,d}={a} となるため、開集合の補集合として閉集合となる。
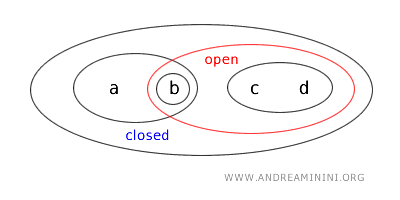
- {a,b} は開かつ閉、いわゆる clopen の例である。これは {a,b} が位相 T で開として与えられ、かつ開集合 X-{c,d} の補集合でもあるため閉集合でもあるからである。
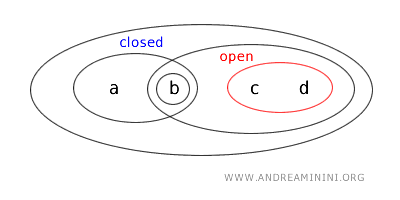
- {b,c} は開でも閉でもない。開集合として定義されておらず、いかなる開集合の補集合にもならないためである。
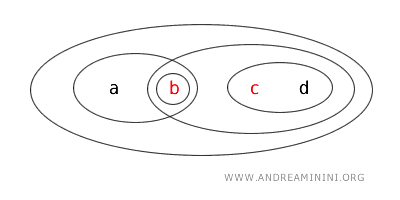
この例から分かるように、位相空間において集合は開、閉、その両方、あるいはそのいずれでもない場合があり得る。
閉集合の性質
閉集合とは、開集合の補集合として定義される集合であり、次の基本的性質を備えている。
- 空集合(Ø)および全空間 X は常に閉集合である。
- 閉集合の任意個の共通部分(交わり)は閉集合である。
- 有限個の閉集合の和集合(結び)は閉集合である。
例:
ユークリッド空間 Rn の標準位相では、任意の 1 点集合は閉集合となる。
実数直線 R1 上の 1 点 n を考えると、その補集合は R1 のうち n を除くすべての点から構成される。
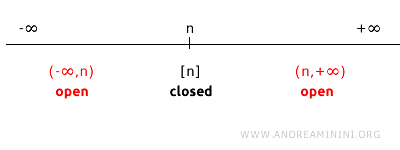
したがって、{n} の補集合は開区間 (-∞, n) と (n, +∞) の和集合 (-∞, n) ∪ (n, +∞) で表される。
標準位相では、(-∞, n) も (n, +∞) も開集合であり、それらの和集合も開集合となる。
ゆえに、その補集合をもつ {n} は閉集合であることが導かれる。
ただし、任意の 1 点集合が常に閉集合となるわけではないことに注意すべきである。閉集合かどうかは空間に与えられた位相に依存する。例えば、整数 n に対して開区間 (n, n+1) を基礎として生成した位相を R 上に与えた場合、この位相では 1 点集合 {n} は閉集合とならない。これはその点の周囲の境界を含まないためである。
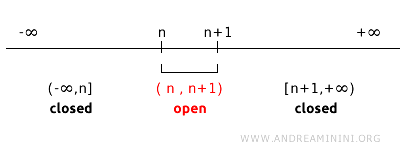
この位相では、(1,2) や (2,3) が開集合である。開集合 (1,2) の補集合は (-∞,1] ∪ [2,+∞) となり、同様に (2,3) の補集合は (-∞,2] ∪ [3,+∞) となる。このように、ある 1 点のみを補集合として得ることはできず、1 点集合 {n} が閉集合とならないことが分かる。一般にこの位相では、任意の開集合 (n, n+1) の補集合は閉区間の和集合 (-∞, n] ∪ [n+1, +∞) となり、結果として 1 点集合は閉集合とは認められない。この例は、閉集合の概念が位相の取り方に本質的に左右されることを示している。
補足事項
以下に、閉集合に関する重要な補足事項をまとめる。
- 閉集合と極限点
集合の極限点とは、どれほど小さな近傍をとっても常にその集合の別の点を含むような点である。閉集合はすべての極限点を含むという特徴をもち、これが開集合との根本的な違いの一つとなる。例: 実数直線上の閉区間 [0,1] を考える。この区間の任意の点、例えば 0.5 のまわりには、[0,1] 内の無数の点を含む開近傍が存在するため、0.5 は極限点である。
![閉区間 [0,1] における 0.5 の極限点の例](/data/andreaminininet/closed-set-example-limit-point-am-net-2024-1.gif)
これは端点についても同様であり、端点 0 の近傍には 0.1、0.01、0.001 などの点が含まれるため、0 も極限点となる。
![閉区間 [0,1] の端点も極限点である例](/data/andreaminininet/closed-set-example-limit-point-am-net-2024-2.gif)
このように、閉区間 [0,1] の各点は必ず同区間の点を多数含む開近傍によって取り囲まれている。 - 集合 A が閉であることの同値条件 A = Cl(A)
位相空間において、集合 \( A \) が閉であるとは、それが自らの閉包と一致すること、すなわち \( A = \text{Cl}(A) \) が成立することである。閉包 \( \text{Cl}(A) \) とは、集合 \( A \) の全ての点と、それに属する極限点をすべて含む集合である。したがって、集合 \( A \) がすべての極限点を含むとき、それは閉集合である。
以上の内容から、閉集合の性質は位相の構造そのものと密接に結びついており、位相空間論を理解するうえで欠かせない概念であることが分かる。