位相変換とは何か？──ドーナツがコーヒーカップに変わる数学の世界

位相変換（Topological Transformation）とは、対象を「壊さず・貼り合わせず」に変形しながら、その根本的なつながり方（連結性）や連続性を保つ変換のことです。

この概念は、数学の中でも「トポロジー（位相幾何学）」という分野の中心テーマです。トポロジーでは、形の大きさや角度よりも、空間がどうつながっているかに注目します。つまり、ものの「かたち」ではなく「構造」を見る学問なのです。

位相変換の基本的な特徴

位相変換には、次のような特徴があります。

連続的な変化であること
小さな変化が滑らかにつながっており、入力の微妙な違いが出力にも連続的に反映されます。
つながり方を保つ
変換によって、空間内の点どうしの「つながり」や「近さ」は保たれます。たとえば、もともと隣同士だった点は、変換後も隣同士のままです。
壊さず・貼らずに変形
引き伸ばしたり、曲げたり、押しつぶしたりすることはできますが、切ったりくっつけたりはできません。
有名な例がドーナツとコーヒーカップです。どちらも穴が1つあるため、位相的には同じ構造を持っています。

💡 応用： 位相変換の考え方は、結び目理論や代数的トポロジーなどの純粋数学はもちろん、物理学やコンピューターグラフィックスなど、さまざまな分野で活用されています。

位相変換といっても、その性質や使われ方によっていくつかの種類に分かれます。

同相写像（Homeomorphism）
ある空間を、切断や接着をせずに別の空間へ変形し、さらに元に戻せるような連続的な変換です。ドーナツとコーヒーカップの例がまさにこれです。
同位（Isotopy）
各段階がすべて同相写像であるような滑らかな変形です。例えば、ひもの結び目を締めず・緩めずに動かすとき、その一連の動きが同位にあたります。
ホモトピー（Homotopy）
一つの写像を、連続的に別の写像へと変形していく概念です。条件は同相より緩く、たとえばバネを引き伸ばして戻すとき、その途中のすべての形はホモトピー的に同じです。
微分同相写像（Diffeomorphism）
同相写像であり、かつ微分可能な滑らかな変換です。これは「微分トポロジー」で重要な概念で、たとえば球体をなめらかに変形して楕円体にするような場合に使われます。

これらの変換は、空間や関数の「滑らかさ」や「変形のしかた」に注目し、トポロジーのさまざまな側面を明らかにする手がかりになります。

よく混同されがちですが、幾何変換（Geometric Transformation）と位相変換は目的も性質も異なります。

幾何変換
物体の形や位置を変える変換で、距離・角度・形状といった幾何的な性質を保ちます。代表的なものには平行移動、回転、反射、拡大・縮小などがあります。
例：回転では距離や角度は変わらず、向きだけが変わります。
位相変換
一方で位相変換は、距離や角度が変わっても、空間の「つながり方」や「連続性」を守ります。柔軟に変形できることが大きな特徴です。
例：ドーナツとコーヒーカップは、形は違っても穴の数（構造）が同じため、位相的には等価です。

幾何変換は数値的な関係（距離・角度・形）を保つのに対し、位相変換は空間の連続性とつながりを保ちます。つまり、「形」は変わっても「構造」は変わらないのです。

実は、両方の性質を持つ変換も存在します。つまり、形や角度を保ちつつ、連続的で位相的にも安定している変換です。

等距変換（Isometry）
平行移動・回転・反射など、点間距離や角度を完全に保つ変換。幾何的にも位相的にも成立し、逆写像も連続なので同相写像の一種といえます。
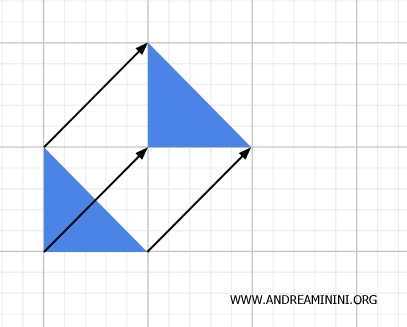
相似変換（Similarity）
角度と比率を保ちながら大きさだけを変える変換です。拡大や縮小がこれにあたり、幾何的にも位相的にも意味をもちます。

このように、トポロジーの世界では「形」を変えても「構造」を変えないという考え方が根底にあります。幾何学とトポロジーは一見別の分野のように見えますが、実はその境界は意外に柔らかいのです。

形は変わっても、本質は変わらない。──それが位相変換の魅力です。