正則空間（正則位相空間）とは何か

正則空間は、よく知られたハウスドルフ空間よりも一段階強い性質をもつ空間です。空間の「分離のしやすさ」をより詳細に捉えたいときに重要となる概念です。

さらに、正則空間が可算基をもつ場合、その空間はウリソーンの距離化定理によって距離付け可能になります。このため、正則性は位相空間の解析において実用的な意味ももちます。

ハウスドルフ空間との違い

ハウスドルフ空間では異なる二点を開集合で分けられますが、正則空間ではさらに一歩進んで、点と閉集合の組を分離できます。この違いは、空間がどこまで精密に対象を区別できるかという「解像度」の差として理解できます。

Note. 正則空間と正規空間は名前が似ていますが、条件は異なります。正規空間では互いに素な二つの閉集合が開集合で分けられる必要があります。このため、正規空間は必ず正則空間ですが、正則空間が正規であるとは限りません。

また、正則性とハウスドルフ性は独立の性質であり、一方を満たしてももう一方を満たすとは限りません。

正則空間の代表例

正則空間のもっとも身近な例は、標準位相を備えた実数直線 \( \mathbb{R} \) です。

例として、点 \( x = 2 \) と次の閉集合 \( C \) を考えます。

\[ C = (-\infty, 0] \cup [5, \infty) \]

この状況では \( 2 \notin C \) であり、閉集合であることも明確です。

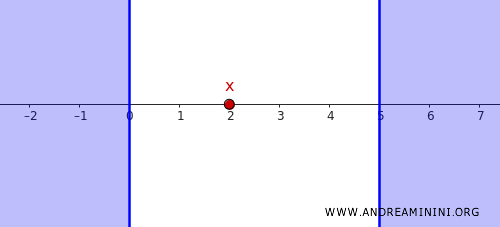
点 \( x \) と閉集合 \( C \) を分離するには、まず \( C \) の補集合の中に含まれる開区間を探します。たとえば、区間 \( (0,5) \) は \( x = 2 \) を含む適切な候補です。

\[ (a, b) = (0, 5) \]

さらに、点 \( x \) をはさむ値 \[ 0 < c < 2 < d < 5 \] を選びます。ここでは \( c = 1 \)、\( d = 3 \) とします。

すると、次の二つの開集合が定義できます。

• \( U = (1,3) \)。これは点 \( x = 2 \) を含みます。
• \( V = (-\infty,1) \cup (3,\infty) \)。こちらは閉集合 \( C \) の全体を覆います。

両者は互いに重ならないため、 \( U \cap V = \emptyset \) が成立します。これで、実数直線が正則空間である理由が具体的に理解できます。

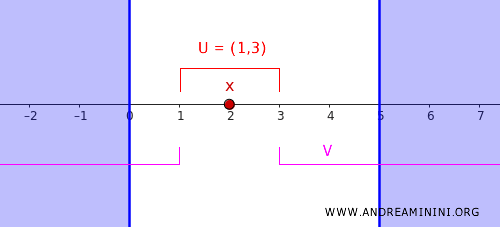
この例は、正則空間の核心である「点と閉集合の分離」が実際にどう機能するのかを示す典型的なケースです。

より深い視点

• 分離公理の体系の中での位置づけ
  正則空間は、位相空間の分離性を判断する一連の公理の中で重要な役割を果たしています。これらの性質を比較することで、空間がどの程度に構造を識別できるかが見えてきます。

  Note. ハウスドルフ性は二点間の分離を扱い、正則性は点と閉集合の分離を扱います。どちらの性質も、空間が内部の対象をどれほど細かく区別できるかという観点から理解すると整理しやすくなります。

ここまで見てきたように、正則空間は位相空間論において基本でありながら奥行きのある概念です。空間の分離性を深く理解したいときに欠かせない重要なテーマといえます。