トポロジーの世界における「つながり」--連結性とは？

トポロジー（位相幾何学）では、空間の「つながり方」に注目します。連結性（connectivity）とは、空間がバラバラに分かれず、一つのまとまりとして存在しているかを表す概念です。言い換えれば、空間内の任意の2点を、外に出ることなく連続した経路で結べるかどうかを調べるものです。

この「つながり」は、トポロジーにおいて連続性と並ぶ基本的な考え方です。図形や空間を、形の変化や切れ目を通じて理解するうえで欠かせない性質といえます。

これは開集合によって定義されるため、位相的性質である。

連結性を調べることで、空間の構造やその内部の要素同士の関係を深く理解できます。数学のさまざまな分野--解析学、幾何学、物理学--においても、空間の分類や性質を考える上で重要な鍵となります。

身近な例で見る「連結空間」

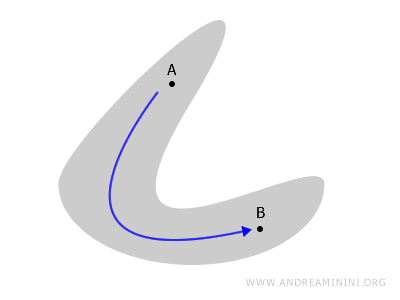
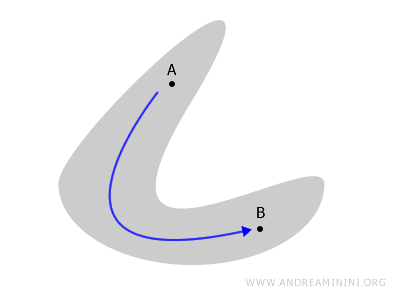
たとえば平面や立体図形を考えましょう。空間の中の2点 A と B を、外に出ることなく連続的に結べるなら、その空間は連結空間です。

反対に、空間がいくつかの部分に分かれており、それぞれの間に行き来できない場合--つまり、どんな道を通っても外に出てしまう場合--その空間は非連結空間です。

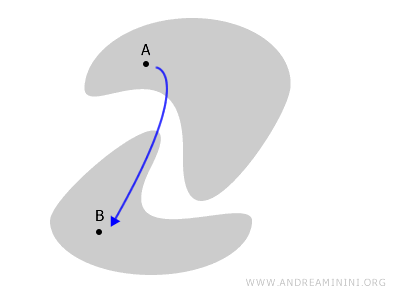
では、もう少し直感的な例で考えてみましょう。

「非連結」ってどんな状態？

建物の中に二つの部屋があり、それぞれ壁で仕切られているとします。これらの部屋は互いに独立した開集合であり、壁という境界は含まれていません。したがって、この空間は非連結です。

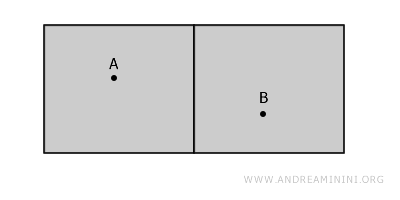
見た目には一つの建物でも、数学的には「つながっていない」のです。なぜなら、A から B に行くためには壁を通り抜けなければならず、壁は空間の外にあるからです。

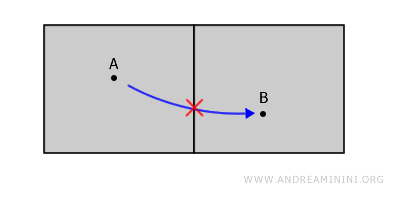
この例からも分かるように、トポロジーでは「境界」は開集合の一部ではないことに注意する必要があります。

局所連結性 -- 小さな範囲での「つながり」

局所連結性（local connectivity）とは、空間全体が分かれていても、各点の近くには小さな「連結な領域」が存在する状態を指します。

先ほどの「二つの部屋」の例を思い出してみましょう。

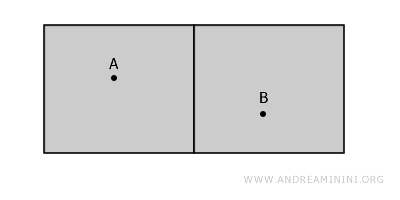
この空間全体では、A と B を壁を越えて結ぶことはできません。しかし、A の周囲の領域だけに注目すれば、その中のすべての点はお互いに連続的に結ばれています。これが局所連結性の典型的な例です。

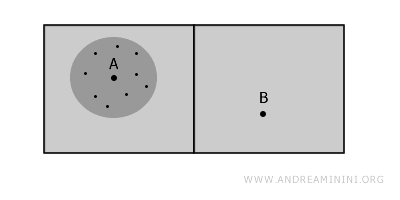
同じことは B の周りにも言えます。つまり、部分的には「つながっている」けれど、全体としては「分かれている」--それが局所連結な空間です。

二つの代表的な「つながり」

トポロジーでよく登場する連結性には、特に重要な二つのタイプがあります。

• 位相的連結性（Topological Connectedness）
  位相空間 $ X $ が 連結 であるとは、空でない2つの開集合 $ U $ と $ V $ が互いに交わらず（$ U \cap V = \emptyset $）、しかもそれらの和が空間全体 $ X $ に等しくなるような組が存在しないことを意味します。
  つまり、空間を「2つの独立した部分」に完全に切り分けることができない場合、その空間は連結と呼ばれます。

  例. 区間 $(-1, 1)$ は連結ですが、$(-1, 0) \cup (0, 1)$ は非連結です。なぜなら、互いに交わらない空でない開集合 $(-1, 0)$ と $(0, 1)$ が存在し、それらの和が空間全体を覆うからです。
  この2つの開集合は、空間の分離（separation）を構成します。

• 道連結性（Path Connectedness ／ 弧状連結性）
  位相空間が道連結であるとは、空間内の任意の2点 A, B に対して、それらを結ぶ連続的な経路（パス）が空間の内部に存在することを指します。
  道連結な空間は常に連結でもありますが、連結であっても道連結でない空間が存在します。

  例. 平面上の閉じた図形を考えてみましょう。図形の内部の任意の2点 A と B は、ペンを紙から離さず、かつ図形の外に出ることなく、連続した曲線で結ぶことができます。
  
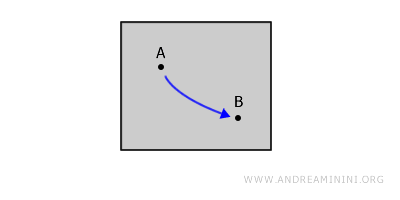
  弧状連結性と道連結性の違い： 弧状連結性は道連結性に似ていますが、経路が1対1対応（単射）である点が異なります。つまり、経路が同じ点を再び通過したり、交差したりしない連続曲線で2点を結ぶ場合を指します。

• 単連結性（Simple Connectivity）
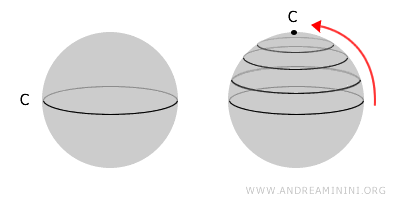
  一方、単連結空間とは、空間内の任意の閉じた曲線を一点まで連続的に縮めることができる空間を指します。つまり、空間の中に「穴」がないということです。単連結空間は常に連結ですが、連結空間が単連結とは限りません。

  たとえば、球面は単連結です。表面上のどんなループも滑らかに一点まで縮めることができるからです。
  それに対して、ドーナツ型のトーラスは内部に穴を持ち、ループを一点まで縮めることができません。つまり、トーラスは連結ではあるが単連結ではない典型的な例です。
  
  
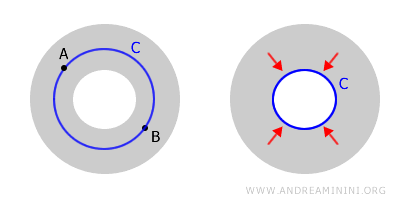
  このように、連結でありながら内部に穴を持つ空間は多重連結空間（multiply connected space）と呼ばれます。環状領域（annulus）はその代表例です。

まとめ -- 数学的な「つながり」を感じる

連結性は、空間の性質を理解するうえでの出発点です。トポロジーでは、「どのように形が変わっても切れずに保たれる関係」を探求します。

• 実数直線上では、連結な集合は区間だけです。

つまり、連結性を理解することは、「世界がどのようにつながっているのか」を数学の言葉で探ることにほかなりません。