閉開集合（Clopen Sets）とは何か

ある集合が同じ位相のもとで開集合と閉集合の両方の性質を持つとき、その集合を「閉開集合（clopen）」と呼びます。

閉開集合は、開集合と閉集合という一見対照的な概念を同時に満たす特殊な集合です。名前は “closed” と “open” を組み合わせた造語で、位相空間に潜む構造を理解する上で重要な役割を果たします。

ある集合とその補集合がどちらも開集合であるとき、その集合は閉開集合となります。

ポイント: 実数全体に通常の位相を入れた場合、閉開集合は空集合や全体集合のように自明なものしか存在しません。しかし別の位相空間では、多様な閉開集合が登場します。空間の特徴をつかむ上で注目すべき概念です。

具体例で理解する

位相 T を入れた集合 X={a,b,c,d} を考えます。

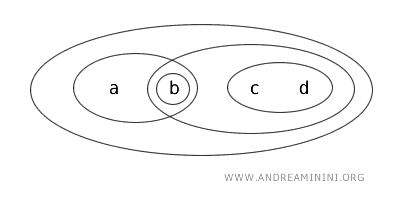
この位相では {b}, {a,b}, {c,d}, {b,c,d}, {a,b,c,d}, そして Ø が開集合です。

したがって部分集合 {a,b} は T における開集合です。

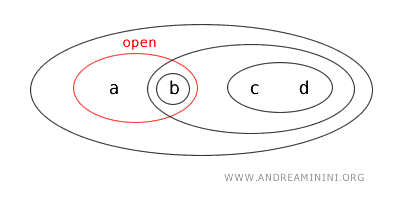
さらに集合 {a,b} は開集合 {c,d} の補集合でもあります。

$$ X - \{ c,d \} = \{a , b \} $$

補集合が開集合なら元の集合は閉集合なので、

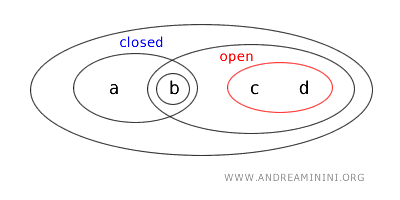
{a,b} は閉集合でもあります。つまりこの位相では {a,b} が閉開集合となります。

空集合と全体集合は必ず閉開集合

どの位相空間でも、空集合 (∅) と全体集合 (X) は例外なく閉開集合です。両方とも開集合であり、同時に閉集合でもあります。

開集合の定義によれば、空集合と全体集合は常に開集合です。

閉集合の定義では、補集合が開集合である場合に閉集合とみなされます。

この二つを組み合わせると次の事実が導かれます。

• 空集合 (∅)
  空集合は開集合であり、その補集合 X は開集合なので閉集合でもあります。
• 全体集合 (X)
  全体集合 X は開集合であり、その補集合 $ X \setminus X=∅ $ は開集合なので閉集合でもあります。

したがってどの位相でも空集合と全体集合は変わらず閉開集合となります。

閉開集合は抽象的に見えて、実は位相空間の性質を見抜くための指標のひとつです。より深く学んでいくと、連結性など他の概念とも密接に関わっていることが分かります。