正規空間とは何か

正規性の特徴は、互いに素な閉集合をきれいに「別々の開集合」に包み込める点にあります。閉集合どうしに接点がなければ、その周囲に重ならない開近傍を整然と与えることができる、というわけです。

この性質は、連続関数を使って集合や点を分離したい場面でとても重要になります。分離公理の体系の中でも、正規空間は特に強い性質を持つ空間として扱われます。

実数直線を例にする

標準位相を備えた実数直線 \( \mathbb{R} \) は、正規空間の最も身近な例です。まずは具体的に見てみましょう。

• \( A = \{0\} \) 一点集合
• \( B = [2, 3] \) 閉区間

この二つは閉集合であり、もちろん互いに交わりません。

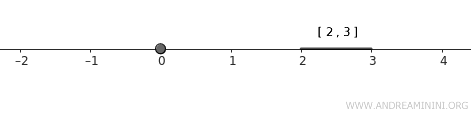
補足。一点集合は閉集合になり、閉区間も端点を含むため閉集合です。

これらを分離するには、互いに素な開集合を次のように取れば十分です。

まず \( A = \{0\} \) を含む開集合

$$ A \subset U = (-1,1) $$

次に \( B = [2,3] \) を含む開集合

$$ B \subset V = (1,4) $$

見てのとおり、\( U \cap V = \emptyset \) が成り立ちます。このシンプルな例からも、実数直線が正規空間の条件を満たしていることがわかります。

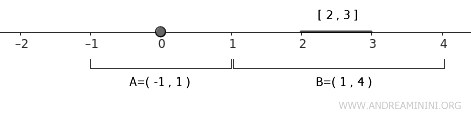
同じやり方で、実数直線上のどんな互いに素な閉集合を選んでも、互いに素な開集合によって分離できます。つまり、標準位相を備えた \( \mathbb{R} \) は典型的な正規空間です。

正規空間について知っておきたいこと

最後に、正規空間を理解するうえで役立つポイントをまとめます。

• 実数直線 \( \mathbb{R} \) は正規空間
  よく知られた性質で、正則性 \( T_3 \) より強い \( T_4 \) を満たします。
• すべての距離空間は正規
  距離が定義されている空間では、集合の分離が容易にできるため正規性が保証されます。
• 正規空間は必ず正則空間
  分離公理の階層の中でも、正規性は正則性を含むより強い条件です。

正規空間は抽象的に見えるかもしれませんが、具体例と合わせて考えると、その構造の整い方や分離のしやすさがよくわかります。