経路連結空間とは何か

位相空間 S が 経路連結（path-connected）であるとは、空間の中にある任意の2点 A と B を、外に出ることなく連続した経路で結ぶことができることを指します。

少しイメージしてみましょう。一枚の紙を思い浮かべてください。その端（境界）は考えないものとします。

この紙は、境界を除いた連続的な領域を表しており、数学的には「開いた」空間と呼ばれます。

紙の上に2つの点 A と B を取ると、ペンを持ち上げずにその2点を線でつなぐことができますね。

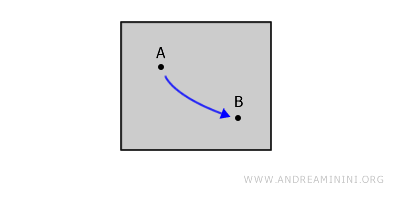
つまり、A と B を結ぶ線（経路）は、常に紙の上にとどまり、外には出ないということです。

このような空間は、必ず「連結」でもあります。

直感的にも納得できるでしょう。もし空間が分かれていれば、空間の外に出ずに2点を結ぶ経路は描けないからです。

ただし、逆は成り立ちません。連結な空間が必ずしも経路連結であるとは限りません。

一見すると不思議ですが、そうした例は実際に存在します。

次の2つの集合を見てみましょう。

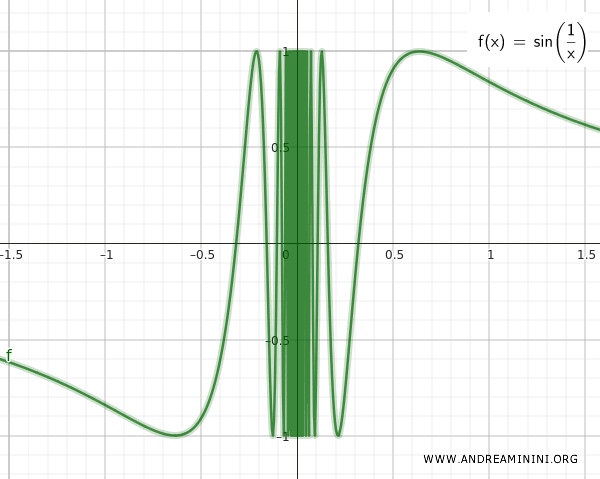
$$ Q = \{ \forall \ x \ \in R-\{ 0 \} \ , \ \sin( \frac{1}{x} ) \} $$

$$ T = \{ \ 0 \} $$

集合 Q は、x ≠ 0 に対して定義された関数 sin(1/x) のグラフ上の点から成ります。x = 0 のときは 1/x が定義できないため、その点だけが抜けています。

一方、集合 T は 0 という1点だけです。

この2つの集合 Q と T は、関数 sin(1/x) のグラフに示されるように、無限に近い距離で寄り添っています。

2つを合わせて作る集合 S は、次のように表されます。

$$ S = Q \cup T $$

集合 S は連結です。なぜなら、どんなに小さい正の数 ε をとっても、0 の近く (0-ε, 0+ε) の範囲には Q の点が必ず存在するからです。

言い換えれば、0 は関数 sin(1/x) の 集積点（accumulation point）になっています。

ところが、この集合 S は経路連結ではありません。なぜなら、Q 上の任意の点と 0（集合 T の点）を連続的な経路で結ぶことはできないからです。

補足: 関数が f(x)=1/x だった場合を考えると、結果はまったく異なります。このとき、Q と T は明らかに分離しており、互いに近接していません。

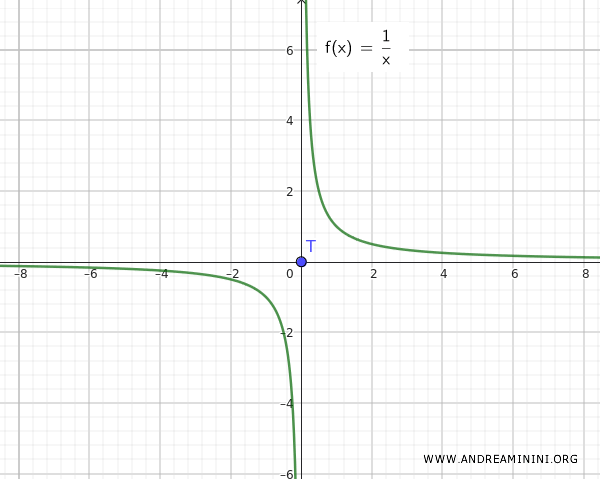
この例からわかるように、連結な集合 Q={∀ x ∈ R-{0}, 1/x} と孤立点 T={0} の和集合は、必ずしも連結とは限りません。孤立点（ここでは 0）が 集積点としても機能しない限り、全体は連結にはならないのです。

このように、経路連結性と単なる連結性とは似て非なる概念であり、その違いを理解することは、位相空間を深く理解するうえで重要です。