内部の共通部分

二つの集合 $A$ と $B$ に対し，それぞれの内部の共通部分は，それらの共通部分の内部と一致する。すなわち，次の等式が成り立つ。$$ \text{Int}(A) \cap \text{Int}(B) = \text{Int}(A \cap B) $$

この結果は位相空間論における基本的かつ重要な性質の一つであり，集合の内部と共通部分の関係を理解するうえで欠かせない。

直感的に言えば，集合 $A$ の内部にある点と，集合 $B$ の内部にある点のうち，両方に同時に含まれる点を集めると，それはそのまま集合 $A \cap B$ の内部を与える。

以下では，この性質を理解するために必要な基本概念を整理し，その後に具体例と証明を示す。

集合の内部（$\text{Int}(A)$）：集合 $A$ に属する点のうち，境界点を除いた点全体である。各内部点のまわりには，完全に $A$ に含まれる開近傍が存在する。
共通部分（$\cap$）：集合 $A$ と集合 $B$ の双方に属する点からなる集合である。

これらを踏まえると，$\text{Int}(A)$ と $\text{Int}(B)$ の共通部分を取る操作は，集合 $A \cap B$ の内部を求めることと本質的に同じであることが分かる。

具体例

部分的に重なり合う二つの円 $A$ と $B$ を考えてみよう。

円 $A$ の内部とは境界を除いた領域全体であり，円 $B$ についても同様である。

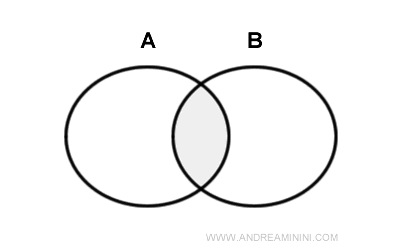
二つの集合の共通部分とその内部を示す図

二つの円の内部どうしの共通部分を取ると，それは円 $A$ と円 $B$ が重なり合っている領域の内部と正確に一致する。この図は，上の等式が自然に成り立つことを視覚的に示している。

この等式は，二つの包含関係をそれぞれ示すことで証明される。

1] 第一の包含（$\subseteq$）

点 $x$ が集合 $A$ の内部に属し，かつ集合 $B$ の内部にも属するとする。このとき，$x$ のまわりには，それぞれ $A$ に完全に含まれる開近傍と，$B$ に完全に含まれる開近傍が存在する。

これら二つの開近傍の共通部分も開集合であり，しかも集合 $A \cap B$ に含まれる。そのため，点 $x$ は集合 $A \cap B$ の内部に属する。

$x \in \text{Int}(A) \cap \text{Int}(B)$ とする。このとき，$x \in \text{Int}(A)$ かつ $x \in \text{Int}(B)$ である。

内部の定義より，$x \in U \subseteq A$ を満たす開近傍 $U$ と，$x \in V \subseteq B$ を満たす開近傍 $V$ が存在する。

ここで $W = U \cap V$ とおく。$U$ と $V$ はいずれも開集合であるため，$W$ も開集合であり，かつ $x$ を含む。

さらに，$W \subseteq U \subseteq A$ および $W \subseteq V \subseteq B$ から，$W \subseteq A \cap B$ が従う。

よって，$x \in \text{Int}(A \cap B)$ である。

以上より，$\text{Int}(A) \cap \text{Int}(B) \subseteq \text{Int}(A \cap B)$ が示された。

2] 第二の包含（$\supseteq$）

次に，点 $x$ が集合 $A \cap B$ の内部に属するとする。このとき，$x$ のまわりには，集合 $A \cap B$ に完全に含まれる開近傍が存在する。

この開近傍は同時に集合 $A$ と集合 $B$ の部分集合でもあるため，点 $x$ は両方の集合の内部に属することになる。

$x \in \text{Int}(A \cap B)$ とする。このとき，$x$ を含み $W \subseteq A \cap B$ を満たす開近傍 $W$ が存在する。

$W \subseteq A \cap B$ であることから，$W \subseteq A$ かつ $W \subseteq B$ が成り立つ。

したがって，$x \in \text{Int}(A)$ かつ $x \in \text{Int}(B)$ である。

よって，$x \in \text{Int}(A) \cap \text{Int}(B)$ が従う。

以上より，$\text{Int}(A \cap B) \subseteq \text{Int}(A) \cap \text{Int}(B)$ が示された。

以上で両方向の包含関係が確認されたため，次の等式が結論として得られる。

\[ \text{Int}(A) \cap \text{Int}(B) = \text{Int}(A \cap B) \]

これにより証明は完了である。

以下同様である。