開集合でも閉集合でもない集合

位相空間では、ある集合が開集合とも閉集合ともみなされない場合がある。これは、その集合がいずれの条件にも当てはまらないことを意味する。

具体的には、対象の集合が開集合として位相に含まれておらず、さらに任意の開集合の補集合としても表せないとき、その集合は開集合でも閉集合でもない。

注記：実数直線のような身近な位相空間では、このような集合を想像しにくい。しかし、より複雑な位相空間では特に珍しいものではない。以下の例を読むことで、この概念をより明確に理解できる。

具体例

集合 X={a,b,c,d} と位相 T を考える。ここで T は次の集合を開集合として含むものとする： {b}, {a,b}, {c,d}, {b,c,d}, {a,b,c,d}, および ∅。

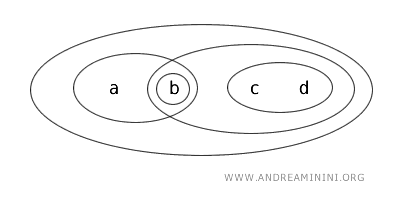
このとき、X の部分集合 {b,c} に注目する。

• {b,c} は、T に含まれる開集合として定義されていないため、開集合ではない。
• また、{b,c} は T におけるどの開集合の補集合にも一致しないため、閉集合でもない。

以上より、位相 T において {b,c} は開集合でも閉集合でもない集合であることがわかる。

このような事例は他の位相空間でも見られ、位相の多様性を理解するうえで重要な視点となる。