داخلية مجموعة

في فضاء طوبولوجي $ X $، تُعرَّف داخلية المجموعة $ A $ بأنها اتحاد جميع المجموعات المفتوحة المحتواة كليًا في $ A $. ويُرمز إليها عادةً بـ $ \text{Int}(A) $ أو $ A^\circ $.

بعبارة بسيطة، تمثّل داخلية المجموعة أكبر جزء مفتوح يمكن العثور عليه داخل $ A $ دون أن يتجاوز حدودها.

ولا توجد أي مجموعة مفتوحة محتواة في $ A $ يمكن أن تكون أوسع من داخلية $ A $.

ملاحظة: بما أن الداخلية تُعرَّف على أنها اتحاد مجموعات مفتوحة، فإنها تكون بالضرورة مجموعة مفتوحة هي الأخرى.

ومن الناحية التعريفية، تتكوّن داخلية المجموعة $ A $ من جميع النقاط التي يمكن إحاطتها بجوار مفتوح يقع بالكامل داخل $ A $.

$$ \text{Int}(A) = \bigcup \{ U \subseteq A : U \text{ مجموعة مفتوحة في } X \} $$

أي أن كل نقطة $ x $ تنتمي إلى داخلية $ A $ تمتلك على الأقل جوارًا مفتوحًا $ U $ يحقق الشرطين $ x \in U $ و $ U \subseteq A $.

من المهم الانتباه إلى أن داخلية المجموعة $ A $ لا تتحدد بخصائص $ A $ وحدها، بل تعتمد أساسًا على البنية الطوبولوجية $ X $. لذلك قد تختلف داخلية المجموعة نفسها عند تغيير الطوبولوجيا.

مثال تطبيقي
مبرهنة داخلية المجموعة
خصائص الداخلية
ملاحظات

مثال تطبيقي

لننظر إلى المجموعة $ A = [0, 1] $ ضمن مجموعة الأعداد الحقيقية $ \mathbb{R} $ المزوَّدة بـ الطوبولوجيا القياسية.

يمثل هذا المجال جميع الأعداد الحقيقية الواقعة بين 0 و1 مع اشتمال الطرفين.

في هذه الحالة، تكون داخلية $ A $ هي المجال المفتوح $ (0, 1) $.

$$ \text{Int}(A) = (0,1) $$

فالعدد 0 والعدد 1 لا ينتميان إلى أي مجال مفتوح يقع بالكامل داخل $ A $، ولهذا يتم استبعادهما من الداخلية.

المثال 2

نأخذ الآن المجموعة $ A = [0, 1) $ في $ \mathbb{R} $ تحت الطوبولوجيا القياسية.

هذا المجال مغلق من جهة 0 ومفتوح من جهة 1.

رغم ذلك، تبقى داخلية $ A $ هي نفسها:

\[ \text{Int}(A) = (0,1) \]

والسبب هو أن الداخلية تُبنى من المجموعات المفتوحة فقط، ولا توجد أي مجموعة مفتوحة محتواة في $ A $ تشمل النقطة 0.

ملاحظة: في $ \mathbb{R} $ مع الطوبولوجيا القياسية، تُعد المجالات المفتوحة الأساس في بناء المجموعات المفتوحة. لذلك فإن $ (0,1) $ هو أكبر مجال مفتوح يمكن احتواؤه داخل $ [0,1) $.

المثال 3

نغيّر الآن الإطار الطوبولوجي، وننظر إلى المجموعة $ A = [0,1) $ ضمن فضاء مزوَّد بـ طوبولوجيا منفصلة.

في الطوبولوجيا المنفصلة، تُعد كل مجموعة جزئية مجموعة مفتوحة.

وبذلك يمكن إحاطة أي نقطة من $ A $ بجوار مفتوح يقع بالكامل داخل $ A $.

في الطوبولوجيا المنفصلة على $ \mathbb{R} $، تُعتبر جميع المجموعات الجزئية مفتوحة، سواء كانت مجالات، أو مجموعات منتهية، أو تراكيب اعتباطية من النقاط. ويشمل ذلك حتى المجموعة $ [0,1) $ نفسها.

بما أن $ A $ مجموعة مفتوحة في هذه الطوبولوجيا، فإن داخليتها تساويها تمامًا.

$$ \text{Int}(A) = A = [0,1) $$

وهذه خاصية عامة للطوبولوجيا المنفصلة: داخلية أي مجموعة تطابق المجموعة نفسها.

ملاحظة: يوضح هذا المثال بجلاء أن مفهوم الجوار والداخلية يتغير جذريًا بتغير الطوبولوجيا، حتى لو بقيت المجموعة نفسها دون تغيير.

المثال 4

لنعتبر فضاءً طوبولوجيًا $ X = \{a, b, c\} $ مزوَّدًا بطوبولوجيا منفصلة.

في هذا الفضاء، تكون كل مجموعة جزئية مفتوحة، بما في ذلك:

المجموعة الخالية $ \emptyset $ والمجموعة الكلية $ \{a,b,c\} $.
المجموعات الأحادية مثل $ \{a\} $، $ \{b\} $، و $ \{c\} $.
المجموعات الثنائية مثل $ \{a,b\} $، $ \{a,c\} $، و $ \{b,c\} $.

لنأخذ المجموعة $ A = \{b, c\} $.

المجموعات المفتوحة المحتواة في $ A $ هي $ \{b\} $، $ \{c\} $، و $ \{b,c\} $.

\[ \text{Int}(A) = \{b\} \cup \{c\} \cup \{b,c\} = \{b,c\} \]

وبالتالي تكون داخلية $ A $ مساوية تمامًا لـ $ A $.

ملاحظة: هذه النتيجة لا تخص هذا المثال فقط، بل تنطبق على أي مجموعة جزئية في فضاء ذي طوبولوجيا منفصلة، حيث تكون كل مجموعة مساوية لداخليتها.

مبرهنة داخلية المجموعة

في فضاء طوبولوجي $ X $، إذا كانت $ S \subseteq X $ مجموعة جزئية وكان $ y \in X $، فإن النقطة $ y $ تنتمي إلى داخلية المجموعة $ S $، ويرمز لها بـ $ \text{Int}(S) $، إذا وفقط إذا وُجدت مجموعة مفتوحة $ U $ تحقق $ y \in U \subseteq S $. وبصيغة رياضية: $$ y \in \text{Int}(S) \iff \exists \ U \text{ مجموعة مفتوحة بحيث } y \in U \subseteq S $$

بعبارة مباشرة وسهلة القراءة، تنتمي النقطة $ y $ إلى داخلية $ S $ عندما يمكن إحاطتها بمجموعة مفتوحة تقع بالكامل داخل $ S $.

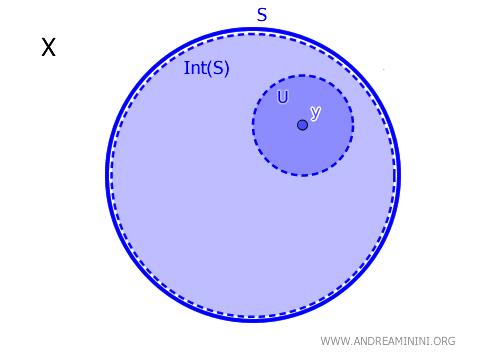
تمثيل بصري يشرح فكرة داخلية مجموعة في فضاء طوبولوجي

تمنحنا هذه المبرهنة معيارًا واضحًا وعمليًا يحدد بدقة متى تكون نقطة ما جزءًا من داخلية مجموعة ضمن فضاء طوبولوجي.

البرهان

الشرط اللازم: إذا كانت $ y \in \text{Int}(S) $، فبحسب تعريف الداخلية توجد مجموعة مفتوحة $ U \subseteq X $ بحيث $ y \in U $ و $ U \subseteq S $. وهذا يحقق الاتجاه الأول من المبرهنة.
الشرط الكافي: إذا وُجدت مجموعة مفتوحة $ U $ تحقق $ y \in U \subseteq S $، فإن جميع نقاط $ U $، ومنها $ y $، تنتمي إلى داخلية $ S $، لأن الداخلية هي اتحاد جميع المجموعات المفتوحة المحتواة في $ S $.

ملاحظة: تكمن أهمية هذه المبرهنة في أنها تربط مفهوم المجموعات المفتوحة مباشرةً بمفهوم الداخلية، وهو ارتباط أساسي في دراسة الاستمرارية وبنية الفضاءات الطوبولوجية.

مثال

لنعتبر المجموعة $ A = [1, 3] $ ضمن مجموعة الأعداد الحقيقية $ \mathbb{R} $ المزوَّدة بالطوبولوجيا القياسية.

$$ A = [1,3] $$

تمثل هذه المجموعة جميع النقاط الواقعة بين 1 و3 مع اشتمال الطرفين.

لتحديد داخلية $ A $، نبحث عن مجموعة مفتوحة $ U $ تكون محتواة بالكامل في $ A $.

اختيار المجموعة $ U $
نأخذ $ U = (1, 3) $، وهو مجال مفتوح لا يشمل النقطتين 1 و3، ولذلك فهو مجموعة مفتوحة في $ \mathbb{R} $.
التحقق من الاحتواء
جميع نقاط $ (1, 3) $ تنتمي إلى $ [1, 3] $، في حين تُستبعد النقطتان الطرفيتان لأن المجال مفتوح.

وبما أن $ U $ مجموعة مفتوحة محتواة كليًا في $ A $، فإن داخلية $ A $ تساوي:

\[ \text{Int}(A) = (1, 3) \]

ملاحظة: لا تنتمي النقطتان 1 و3 إلى داخلية $ A $، إذ لا توجد أي مجموعة مفتوحة تحتوي إحداهما وتقع بالكامل داخل $ A $.

خصائص الداخلية

فيما يلي مجموعة من الخصائص المهمة التي توضح سلوك داخلية المجموعات في الفضاءات الطوبولوجية، وتكشف عن علاقاتها بالاتحاد والتقاطع والإغلاق.

اتحاد الداخليتين
اتحاد داخلية مجموعتين يكون دائمًا محتوى داخل داخلية اتحادهما: $$ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B) $$
تقاطع الداخليتين
داخلية التقاطع تساوي تقاطع الداخليتين: $$ \text{Int}(A) \cap \text{Int}(B) = \text{Int}(A \cap B) $$
داخلية المتمم ومتمم الإغلاق
داخلية متمم مجموعة تساوي متمم إغلاقها: $$ \text{Int}(X - A) = X - \text{Cl}(A) $$
إغلاق المتمم ومتمم الداخلية
إغلاق متمم مجموعة يساوي متمم داخليتها: $$ \text{Cl}(X - A) = X - \text{Int}(A) $$

ملاحظات

نختم ببعض الملاحظات المفيدة التي تساعد على ترسيخ الفكرة:

إذا كانت $ U $ مجموعة مفتوحة في $ X $ و $ U \subseteq A $، فإن $ U \subseteq \text{Int}(A) $
لأن داخلية $ A $ هي أكبر مجموعة مفتوحة محتواة فيها، فإن أي مجموعة مفتوحة داخل $ A $ تكون جزءًا من داخليتها.
إذا كان $ A \subseteq B $، فإن $ \text{Int}(A) \subseteq \text{Int}(B) $
تأخذ عملية الداخلية علاقة الاحتواء بين المجموعات وتحافظ عليها.
المجموعة $ A $ مفتوحة إذا وفقط إذا $ A = \text{Int}(A) $
أي أن كل نقطة في $ A $ تمتلك جوارًا مفتوحًا يقع بالكامل داخلها.
حساب داخلية مجموعة باستخدام لغة R
يمكن الاستفادة من لغة R في تحليل المفاهيم الطوبولوجية وحساب داخلية المجموعات برمجيًا.

تشكل هذه النتائج أساسًا متينًا لفهم مفهوم داخلية المجموعة ودوره المحوري في الطوبولوجيا.