الطوبولوجيا القياسية على مجموعة الأعداد الحقيقية

تُعرّف الطوبولوجيا القياسية على مجموعة الأعداد الحقيقية ℝ بأنها تضم جميع الفترات المفتوحة (a, b) حيث a < b، إضافةً إلى أي اتحاد نهائي أو غير نهائي لهذه الفترات. وتُعتبر هذه الفترات مجموعات مفتوحة ضمن هذا الإطار.

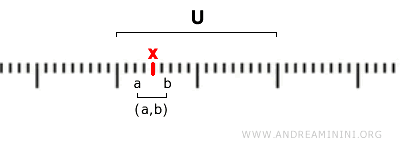
بمعنى آخر، تكون المجموعة U مفتوحة إذا تحقق الشرط التالي: لكل نقطة x تنتمي إلى U، توجد فترة مفتوحة (a, b) تحتوي هذه النقطة وتقع بالكامل داخل المجموعة U.

$$ x \in (a,b) \subseteq U $$

وهذا يعني أن كل عنصر x من المجموعة المفتوحة U يوجد ضمن فترة مفتوحة (a, b) تنتمي أيضاً إلى U.

وبناءً على ذلك، يمكن تحديد المجموعات المفتوحة في الطوبولوجيا القياسية على النحو التالي:

• الفترات المفتوحة
  تُعرَّف المجموعات المفتوحة في ℝ بأنها جميع الفترات المفتوحة \( (a, b) \) حيث a < b، وأي اتحاد لهذه الفترات، سواء كان محدوداً أم غير محدود.
• عمليات المجموعات
  تشمل المجموعات المفتوحة أيضاً نتائج عمليتي الاتحاد والتقاطع المحدود بين المجموعات المفتوحة.
  • الاتحاد: اتحاد أي عدد من المجموعات المفتوحة يُعتبر دائماً مجموعة مفتوحة.
  • التقاطع المحدود: تقاطع عدد محدود من المجموعات المفتوحة يُنتج أيضاً مجموعة مفتوحة.

تُعد الطوبولوجيا القياسية واحدة من أشهر الطوبولوجيات الممكن تعريفها على مجموعة الأعداد الحقيقية، وسُمّيت "قياسية" لأنها الأكثر استخداماً وانتشاراً في مختلف فروع الرياضيات.

ويرجع ذلك إلى قدرتها على تمثيل المفاهيم الأساسية للقرب والانفتاح والاستمرارية بصورة بديهية، مما يجعلها الأساس في دراسة التحليل الرياضي والطوبولوجيا العامة.

ملاحظة: قد تُعرَّف طوبولوجيات أخرى على ℝ أو على مجموعات مختلفة باستخدام أسس متنوعة، مما يؤدي إلى قواعد مغايرة لتحديد المجموعات المفتوحة. وغالباً ما تُستخدم هذه الطوبولوجيات البديلة لاستكشاف خصائص خاصة أو لدراسة حالات رياضية معينة.

مثال تطبيقي

تشمل قاعدة الطوبولوجيا القياسية على خط الأعداد الحقيقية ℝ جميع الفترات المفتوحة (a, b) التي يتحقق فيها a < b.

$$ B = \{ (a,b) \subset; R \ | \ a \lt b \} $$

ومن الخصائص الأساسية لهذه الطوبولوجيا أنه لأي نقطة x داخل فترة مفتوحة يمكن إيجاد فترة مفتوحة أصغر تحتوي هذه النقطة وتقع بالكامل ضمن الفترة الأصلية، وبذلك يتحقق تعريف المجموعة المفتوحة.

$$ \forall \ x \ \in U \ \exists \ \epsilon>0 \ | \ x \in (x-\epsilon, x+\epsilon) \subseteq U $$

حيث إن U مجموعة مفتوحة وفقاً للطوبولوجيا القياسية على ℝ، وهي الطوبولوجيا الأكثر شيوعاً على خط الأعداد الحقيقية.

مثال 2

لنأخذ الفترة (0,1) التي لا تشمل الطرفين 0 و1، ونطبّق عليها الطوبولوجيا القياسية. نريد معرفة ما إذا كانت هذه الفترة تشكّل فضاءً طوبولوجياً.

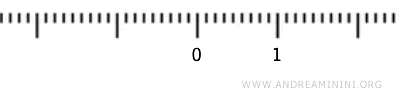
عملياً، تكون المجموعة \( U \subset (0, 1) \) مفتوحة في \( (0, 1) \) إذا وُجدت لكل نقطة \( x \in U \) فترة مفتوحة \( (a, b) \) في ℝ بحيث \( x \in (a, b) \) و \( (a, b) \cap (0, 1) \subseteq U \).

وبذلك يمكن اعتبار الفترة (0,1) نتيجة لتقاطع مجموعات مفتوحة من الطوبولوجيا القياسية على ℝ.

إذن، الفترة \( (0, 1) \) تُعتبر فضاءً طوبولوجياً وفق الطوبولوجيا المستحثة من الطوبولوجيا القياسية على \( \mathbb{R} \).

على سبيل المثال، الفترات \( (0.1, 0.5) \) و\( (0.2, 0.9) \) أو اتحادها مثل \( (0.1, 0.5) \cup (0.6, 0.8) \) جميعها تُعد مجموعات مفتوحة داخل \( (0, 1) \) وفق الطوبولوجيا المستحثة. أي أن المجموعات المفتوحة داخل \( (0, 1) \) هي نفسها المجموعات المفتوحة في ℝ ولكن محصورة داخل الفترة \( (0, 1) \).

وبما أن \( (0, 1) \) فضاء جزئي من ℝ وفق الطوبولوجيا المستحثة، فإنه يحتفظ بجميع الخصائص الأساسية للفضاء الطوبولوجي.

مثال 3

لنفترض أن لدينا المجموعة المنتهية X={1,2,3} التي تضم ثلاثة أعداد صحيحة. نريد معرفة ما إذا كان يمكن اعتبارها فضاءً طوبولوجياً وفق الطوبولوجيا القياسية على \( \mathbb{R} \).

في هذه الحالة، لا تُعتبر العناصر المفردة من X مجموعات مفتوحة، لأن الطوبولوجيا القياسية على ℝ تُبنى على الفترات المفتوحة كأساس للمجموعات المفتوحة، وهذا لا ينطبق مباشرة على المجموعة X.

على سبيل المثال، إذا اعتبرنا العنصر {2} في المجموعة X عدداً حقيقياً، فإنه يقع ضمن فترة مفتوحة (2-ε, 2+ε)، غير أن النقاط داخل هذه الفترة هي أعداد حقيقية أخرى لا تنتمي إلى X، وبالتالي لا يتحقق تعريف المجموعة المفتوحة في ℝ.

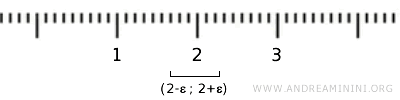
وعند اعتبار \( X \) مجموعة جزئية من ℝ، فإن اعتماد "الطوبولوجيا المستحثة" أو "طوبولوجيا الفضاء الجزئي" على \( X \) يجعل المجموعات المفتوحة مقتصرة على المجموعة الفارغة والمجموعة \( X \) نفسها، مما يقلل من أهميتها الطوبولوجية.

أما في حالة المجموعات المنتهية مثل \( X \)، فيُفضَّل استخدام الطوبولوجيا المنفصلة، حيث تُعتبر كل مجموعة جزئية من \( X \) مفتوحة بالتعريف.

وبذلك يتضح كيف يمكن للطوبولوجيا القياسية أن تشكّل أساساً لفهم مختلف البنى الطوبولوجية الممكنة.