الطوبولوجيا المنفصلة

الطوبولوجيا المنفصلة هي أبسط وأوسع طوبولوجيا يمكن تعريفها على أي مجموعة X، لأنها تشمل جميع المجموعات الجزئية الممكنة من X دون استثناء.

في هذا النوع من الطوبولوجيا، تُعتبر كل مجموعة جزئية من X مجموعة مفتوحة. بمعنى آخر، لا يوجد أي قيد على ما يمكن اعتباره مفتوحاً داخل الفضاء.

كل عنصر في X يُعد بحد ذاته مفتوحاً، مما يجعل كل نقطة مستقلة تماماً عن الأخرى. يمكن تخيّل الفضاء كشبكة من النقاط المنفصلة التي لا تربط بينها أي صلات أو حدود مشتركة.

هذه الفكرة تعكس جوهر الطوبولوجيا المنفصلة: لا يوجد مفهوم "للقرب" بين العناصر، فجميع التوزيعات ممكنة ومقبولة.

وسُميت هذه الطوبولوجيا "منفصلة" لأنها تتعامل مع عناصر X ككيانات مستقلة تماماً، من دون أي تواصل أو استمرارية بينها.

إنها أكبر طوبولوجيا يمكن تعريفها على مجموعة، لأنه لا يمكن إنشاء طوبولوجيا تحتوي على مجموعات مفتوحة أكثر منها، فهي تشمل بالفعل جميع المجموعات الجزئية الممكنة.

ملاحظة: تضع هذه الشروط الأساس الذي يسمح بدراسة مفاهيم القرب والاتصال في الفضاء، أي الاستمرارية، وهي أحد المفاهيم الجوهرية في الطوبولوجيا.

خاصية أساسية

في الطوبولوجيا المنفصلة، كل مجموعة جزئية من الفضاء الطوبولوجي مفتوحة ومغلقة في الوقت نفسه.

ذلك لأن جميع المجموعات الجزئية تُعتبر مفتوحة، وبالتالي فإن متمم أي مجموعة جزئية هو أيضاً مجموعة مفتوحة، مما يجعل المجموعة الأصلية مغلقة كذلك.

في الطوبولوجيا، تُعد المجموعة مغلقة إذا كان متممها مفتوحاً.

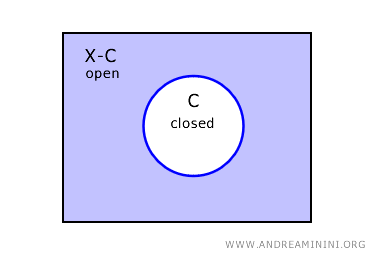
وبما أن كل متمم في الطوبولوجيا المنفصلة مفتوح، فإن كل مجموعة جزئية تكون بالضرورة مغلقة أيضاً. لهذا تُعرف مجموعات هذا الفضاء بأنها مفتوحة ومغلقة معاً، أي كلوبن (clopen).

مثال عملي

لنوضّح الفكرة من خلال مثال بسيط. لنفترض أن لدينا مجموعة منتهية:

$$ X = \{a, b, c\} $$

تُعرف مجموعة القوى لـ X بأنها مجموعة جميع المجموعات الجزئية الممكنة لـ X، وهي كما يلي:

• المجموعة الفارغة: \(\emptyset\)
• المجموعات ذات العنصر الواحد: \(\{a\}\)، \(\{b\}\)، \(\{c\}\)
• المجموعات ذات عنصرين: \(\{a, b\}\)، \(\{a, c\}\)، \(\{b, c\}\)
• المجموعة الكاملة: \(\{a, b, c\}\)

في الطوبولوجيا المنفصلة على X، كل هذه المجموعات تُعتبر مفتوحة. إذن، تكون الطوبولوجيا:

$$ T = \{\emptyset, \{a\}, \{b\}, \{c\}, \{a, b\}, \{a, c\}, \{b, c\}, \{a, b, c\}\} $$

بذلك تكون جميع المجموعات الجزئية لـ \(X\) مفتوحة حسب التعريف، ولا توجد أي قيود على العلاقات بين عناصرها.

لنأخذ مثالاً بسيطاً: المجموعة $ \{ a \} $.

بحسب تعريف الطوبولوجيا المنفصلة، فهي مجموعة مفتوحة. في الوقت نفسه، تُعد مغلقة لأن متممها $ X / \{a\} = \{b, c\} $ هو مجموعة مفتوحة أيضاً. وبالتالي فهي مفتوحة ومغلقة في آن واحد.

وهذا ما يميز الطوبولوجيا المنفصلة: كل مجموعة جزئية فيها مفتوحة ومغلقة في الوقت نفسه.

وينطبق ذلك على كل المجموعات الجزئية الأخرى في الفضاء، دون استثناء.