إغلاق مجموعة
يُقصد بـ إغلاق مجموعة \( A \) في فضاء طوبولوجي \( X \) تقاطع جميع المجموعات المغلقة التي تحتوي \( A \). ويُرمز إلى هذا الإغلاق بالرمز \( \text{Cl}(A) \).
بعبارة بسيطة، إغلاق المجموعة \( A \) هو أصغر مجموعة مغلقة يمكن أن تحتويها بالكامل.
ولا يمكن إيجاد مجموعة مغلقة تحتوي \( A \) وتكون أصغر من إغلاقها.
ملاحظة: تنبع هذه الفكرة مباشرة من التعريف، إذ يُنشأ الإغلاق من خلال تقاطع جميع المجموعات المغلقة التي تضم \( A \). وبهذا المعنى، فإن إغلاق المجموعة هو أقرب إطار مغلق يحيط بـ \( A \)، ويتكوّن من العناصر المشتركة بين كل مجموعة مغلقة تحتويها.
بصيغة رياضية دقيقة، يُكتب إغلاق المجموعة \( A \) على النحو التالي:
$$ \text{Cl}(A) = \bigcap \{ C \subseteq X : A \subseteq C \text{ و } C \text{ مجموعة مغلقة في } X \} $$
حيث يشير الرمز \( \text{Cl}(A) \) إلى إغلاق \( A \)، بينما يعبّر \( \bigcap \) عن عملية التقاطع بين جميع المجموعات المغلقة \( C \) التي تحتوي \( A \).
ويتضمن إغلاق \( A \) عناصر \( A \) نفسها، إضافة إلى جميع نقاطها الحدّية داخل الفضاء \( X \).
ملاحظة: من المهم الانتباه إلى أن إغلاق المجموعة \( A \) يتحدد أساسًا بواسطة الطوبولوجيا المختارة للفضاء \( X \)، وليس بخصائص \( A \) وحدها. ولهذا السبب قد يختلف إغلاق المجموعة نفسها عند تغيير الطوبولوجيا.
مثال توضيحي
لنأخذ المجموعة \( A = (0, 1) \) ضمن مجموعة الأعداد الحقيقية \( \mathbb{R} \) مع الطوبولوجيا القياسية.
تمثل هذه المجموعة فاصلًا مفتوحًا يضم جميع الأعداد الحقيقية بين 0 و1 دون تضمين الطرفين.
في هذه الحالة، يكون إغلاق \( A \) هو الفاصل المغلق \( [0, 1] \).
$$ \text{Cl}(A) = [0,1] $$
أي إن الإغلاق يضم الفاصل المفتوح \( (0,1) \) إضافة إلى نقطتي التراكم عند الحدود، وهما 0 و1.
ملاحظة: في الطوبولوجيا القياسية على \( \mathbb{R} \)، تُعد المجموعة مغلقة إذا كانت تحتوي جميع نقاطها الحدّية. فعلى سبيل المثال، فإن تقاطع الفاصلين المغلقين [0,2] و[-1,1] هو [0,1]. $$ [0,2] \cap [-1,1]=[0,1] $$ ولا يوجد فاصل مغلق أصغر يمكنه احتواء الفاصل المفتوح (0,1).
المثال 2
لننظر إلى المجموعة \( A = [0, 1) \) في \( \mathbb{R} \) مع الطوبولوجيا القياسية.
تضم هذه المجموعة العدد 0، لكنها لا تضم العدد 1، ولذلك فهي فاصل مغلق من اليسار ومفتوح من اليمين.
كما في المثال السابق، يكون إغلاق هذه المجموعة هو \( [0,1] \).
$$ \text{Cl}(A) = [0,1] $$
والسبب أن النقطة 0 موجودة بالفعل في \( A \)، بينما تمثل النقطة 1 نقطة حدّية خارجية يجب إضافتها للحصول على مجموعة مغلقة.
ملاحظة: ينسجم هذا تمامًا مع مفهوم الإغلاق في الطوبولوجيا، حيث تُضاف جميع نقاط التراكم إلى المجموعة. فعلى سبيل المثال، فإن تقاطع [0,2] و[-1,1] يعطي [0,1]. $$ [0,2] \cap [-1,1]=[0,1] $$
المثال 3
لنعد الآن إلى المجموعة نفسها \( A = [0,1) \)، ولكن هذه المرة ضمن فضاء \( X \) مزوّد بـ الطوبولوجيا المنفصلة.
في الطوبولوجيا المنفصلة، تُعد كل مجموعة جزئية من الفضاء مجموعة مفتوحة ومغلقة في الوقت نفسه.
- مجموعة مفتوحة
بما أن كل مجموعة جزئية من \( X \) مفتوحة، فإن \( A \) تُعد مجموعة مفتوحة. - مجموعة مغلقة
وبما أن متممة أي مجموعة جزئية تكون مفتوحة، فإن \( A \) تُعد مغلقة أيضًا.
هذا يعني أن كل مجموعة في الطوبولوجيا المنفصلة تكون مفتوحة ومغلقة معًا.
ونتيجة لذلك، لا يحتاج إغلاق \( A \) إلى إضافة أي عناصر جديدة، فيكون:
$$ \text{Cl}(A) = [0,1) $$
أي إن أصغر مجموعة مغلقة تحتوي \( A \) هي \( A \) نفسها.
ملاحظة: يوضح هذا المثال بجلاء كيف يؤثر اختيار الطوبولوجيا في مفهوم الإغلاق. فالإغلاق لا يعتمد على شكل المجموعة فقط، بل على البنية الطوبولوجية للفضاء الذي تُدرس فيه.
المثال 4
لنعتبر فضاءً طوبولوجيًا \( X \) مكوّنًا من العناصر \( \{a, b, c \} \)، ومزوّدًا بطوبولوجيا منفصلة.
في هذه الحالة، تكون جميع المجموعات الجزئية من \( X \) مفتوحة، بما في ذلك:
- \( \emptyset \) و \( \{a, b, c \} \).
- المجموعات المفردة \( \{a\} \)، \( \{b\} \)، \( \{c\} \).
- وأي اتحاد بينها، مثل \( \{a, b\} \)، \( \{a, c\} \)، \( \{b, c\} \).
وبما أن متممة كل مجموعة جزئية تكون مفتوحة، فإن جميع هذه المجموعات تكون مغلقة أيضًا.
أي إن كل مجموعة في الطوبولوجيا المنفصلة مفتوحة ومغلقة في آن واحد.
إذا أخذنا المجموعة \( A = \{b, c\} \)، فإنها مفتوحة ومغلقة في الوقت نفسه، وبالتالي لا يحتاج إغلاقها إلى إضافة أي عناصر.
\[ Cl(A) = \{b, c\} \]
في هذا النوع من الطوبولوجيا، تكون جميع المجموعات مكتملة من حيث الإغلاق، ولا توجد حاجة إلى أي تعديل إضافي.
ملاحظة: للتحقق السريع، فإن المجموعات المغلقة التي تحتوي \( A \) هي \( \{b, c\} \) و \( \{a,b,c\} \). $$ Cl(A) = \{b,c\} \cap \{a,b,c\} = \{b, c\} $$ وهو ما يبيّن بوضوح أن \( Cl(A) = A \).
مبرهنة إغلاق مجموعة
في فضاء طوبولوجي \( X \)، يُقال إن عنصرًا \( y \) ينتمي إلى إغلاق مجموعة جزئية \( S \)، ويرمز إليه بـ \( \text{Cl}(S) \)، إذا وفقط إذا كان كل مجموعة مفتوحة \( U \) تحتوي \( y \) تتقاطع مع \( S \) تقاطعًا غير فارغ: \( y \in \text{Cl}(S) \iff \forall \, U \text{ مجموعة مفتوحة بحيث } y \in U,\ U \cap S \neq \emptyset \).
بصيغة أبسط، تكون النقطة \( y \) ضمن إغلاق \( S \) إذا كان كل جوار مفتوح لها يلتقي بالمجموعة \( S \).
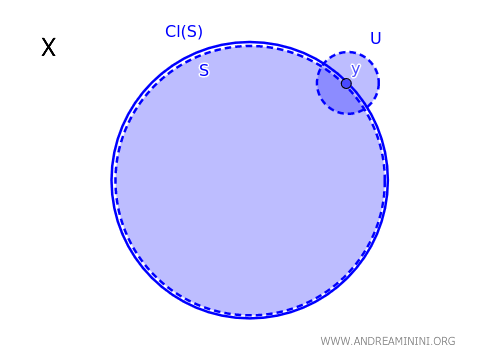
تقدّم هذه المبرهنة أداة عملية وسهلة الاستخدام لتحديد ما إذا كانت نقطة ما تنتمي إلى إغلاق مجموعة في فضاء طوبولوجي، دون الحاجة إلى الرجوع مباشرة إلى تعريف الإغلاق بواسطة المجموعات المغلقة.
البرهان
- الشرط الضروري: إذا كانت \( y \) ضمن إغلاق \( S \)، فإن كل مجموعة مفتوحة تحتوي \( y \) لا بد أن تتقاطع مع \( S \). فالإغلاق يشمل عناصر المجموعة نفسها إضافة إلى نقاطها الحدّية، ونقطة الحدّ هي نقطة لا يمكن فصلها عن المجموعة بواسطة جوار مفتوح.
- الشرط الكافي: إذا كان كل جوار مفتوح للنقطة \( y \) يتقاطع مع \( S \)، فإن \( y \) إما عنصر في \( S \) أو نقطة حدّية لها. وفي كلتا الحالتين، تنتمي \( y \) إلى إغلاق \( S \).
ملاحظة: تُعد هذه المبرهنة من الركائز الأساسية في الطوبولوجيا، لأنها تربط بين مفهوم الجوار المفتوح ومفهوم الإغلاق. ولهذا السبب تُستخدم بكثرة في دراسة الاستمرارية، وتقارب المتتاليات، والخصائص البنيوية للفضاءات الطوبولوجية.
مثال
لنعتبر المجموعة \( A = (0, 2) \) ضمن الطوبولوجيا القياسية على مجموعة الأعداد الحقيقية \( \mathbb{R} \). تمثل هذه المجموعة فاصلًا مفتوحًا على المستقيم الحقيقي.
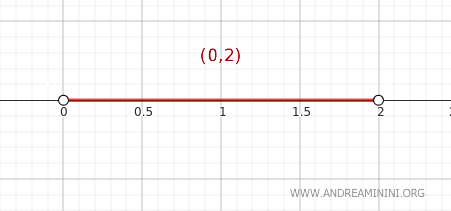
نريد التحقق مما إذا كانت النقطة \( y = 2 \) تنتمي إلى إغلاق \( A \).
تنص المبرهنة على أن ذلك يحدث إذا كان كل جوار مفتوح للنقطة \( y \) يتقاطع مع \( A \).
- فحص الجوار المفتوح: أي فاصل مفتوح يحتوي \( 2 \)، مثل \( (1.9, 2.1) \) أو \( (1.99, 2.01) \)، يحتوي نقاطًا أصغر من 2 وأكبر من 0، وهي نقاط تنتمي إلى \( A \).
- التحقق من التقاطع: بما أن هذا الأمر صحيح لكل جوار مفتوح للنقطة \( 2 \)، فإن شرط المبرهنة متحقق.
وبالتالي نستنتج أن:
$$ y \in \text{Cl}(A) $$
وبالفعل، فإن إغلاق المجموعة \( A \) هو الفاصل المغلق \( \text{Cl}(A) = [0, 2] \)، الذي يحتوي النقطة \( y = 2 \).
خصائص الإغلاق في الفضاءات الطوبولوجية
فيما يلي مجموعة من الخصائص المهمة التي تساعد على فهم سلوك عملية الإغلاق وعلاقتها بعمليات طوبولوجية أخرى مثل الداخل والمتممة.
- داخل المتممة ومتممة الإغلاق
داخل متممة مجموعة \( A \) يساوي متممة إغلاقها: $$ \operatorname{Int}(X - A) = X - \operatorname{Cl}(A) $$ - إغلاق المتممة ومتممة الداخل
إغلاق متممة \( A \) يساوي متممة داخل \( A \): $$ \operatorname{Cl}(X - A) = X - \operatorname{Int}(A) $$
ملاحظات أساسية
تلخّص النقاط التالية أهم الخصائص العامة لإغلاق المجموعات:
- إذا كانت C مغلقة و A ⊆ C، فإن Cl(A) ⊆ C
لأن الإغلاق هو أصغر مجموعة مغلقة تحتوي \( A \)، فلا يمكن أن يتجاوز أي مجموعة مغلقة تحتويها مسبقًا. - إذا كان A ⊆ B، فإن Cl(A) ⊆ Cl(B)
تضمّن مجموعة داخل أخرى يؤدي إلى تضمّن إغلاقها داخل إغلاق المجموعة الأكبر. - تكون المجموعة مغلقة إذا وفقط إذا A = Cl(A)
أي إذا كانت تحتوي جميع نقاطها الحدّية. - إغلاق المجموعة هو اتحادها مع نقاطها الحدّية
$$ \text{Cl}(A) = A \cup A' $$ - خاصية التكرار
تطبيق الإغلاق أكثر من مرة لا يغيّر النتيجة: $$ \text{Cl}(\text{Cl}(A)) = \text{Cl}(A) $$ - خاصية الاحتواء
كل مجموعة محتواة دائمًا في إغلاقها: $$ A \subseteq \text{Cl}(A) $$
يتبع المزيد.