مفهوم الاتصال في علم الطوبولوجيا

في علم الطوبولوجيا، نصف الفضاء بأنه متصل عندما لا يمكن تقسيمه إلى مجموعتين مفتوحتين منفصلتين عن بعضهما. وبعبارة أبسط، يعني الاتصال أن كل نقطتين داخل الفضاء يمكن ربطهما بمسار مستمر دون الخروج من حدوده.

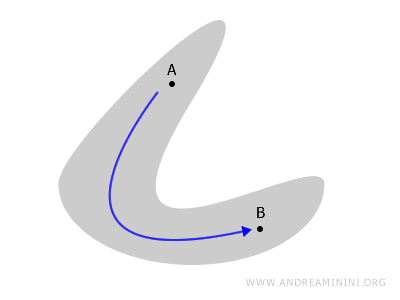
يُظهر مفهوم الاتصال مدى ترابط أجزاء الفضاء الطوبولوجي أو انفصالها عن بعضها. إنه من المفاهيم الجوهرية في الطوبولوجيا إلى جانب الاستمرارية، لأنه يساعدنا على فهم الشكل العام للفضاء وليس فقط تفاصيله الدقيقة.

هي خاصية طوبولوجية لأنها معرّفة بدلالة المجموعات المفتوحة.

يُعد الاتصال عنصرًا أساسيًا في كثير من مجالات الرياضيات، إذ يساعدنا على تحليل بنية الفضاءات والعلاقات بين مكوناتها، ويسهم في تصنيفها وفهم خصائصها الجوهرية.

مثال بسيط لتوضيح الفكرة

تخيّل فضاءً على شكل سطح أو مجسّم. يُعتبر هذا الفضاء متصلًا إذا كان بالإمكان رسم مسار مستمر بين أي نقطتين داخله دون مغادرته.

لكن إن كان الفضاء مكوَّنًا من أجزاء منفصلة عن بعضها، فلا يمكن لأي مسار أن يربط بين هذه الأجزاء دون الخروج منها. عندها نقول إن الفضاء غير متصل.

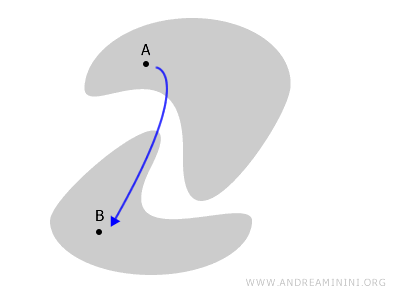
في هذا الشكل، أي محاولة للربط بين النقطتين A وB ستجبرنا على مغادرة الفضاء نفسه. لذا فهو غير متصل.

كيف نفهم الفضاءات غير المتصلة؟

تخيّل مبنى يحتوي على غرفتين منفصلتين يفصلهما جدار. تمثل كل غرفة مجموعة مفتوحة لا تحتوي على الجدار نفسه. ورغم أن الغرفتين في مبنى واحد، إلا أنه لا يمكن الانتقال من واحدة إلى الأخرى دون عبور الجدار - وهو خارج الفضاء المُعرّف.

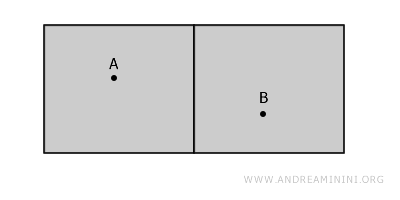
إذن، رغم أن الغرفتين تبدوان متصلتين في الظاهر، إلا أنهما في الحقيقة غير متصلتين. فكل مسار بين النقطتين A وB سيضطر للمرور عبر الجدار.

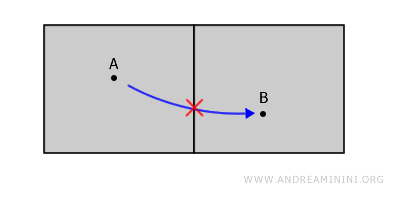
من المهم أن نتذكر أن الحدود، مثل الجدران في هذا المثال، لا تُعتبر جزءًا من المجموعات المفتوحة.

الاتصال الموضعي: رؤية من الداخل

يُقال إن الفضاء يتمتع بـاتصال موضعي عندما تكون كل مجموعة مفتوحة فيه، حتى إن كانت منفصلة عن غيرها، تحتوي على منطقة صغيرة متصلة. أي أن كل نقطة في الفضاء تنتمي إلى جوار متصل بها.

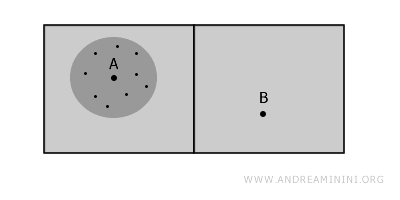
على سبيل المثال، في فضاء مكوَّن من غرفتين منفصلتين، لا يمكن ربط النقطة A بالنقطة B دون عبور الجدار، لكن داخل كل غرفة توجد مناطق متصلة تمامًا.

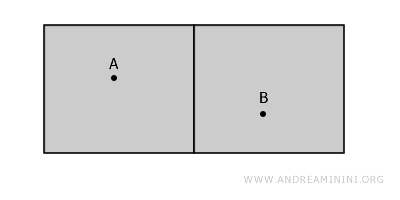
النقطة A مثلًا تقع داخل منطقة متصلة بجميع نقاطها، ما يجعلها مثالًا على الاتصال الموضعي. والأمر نفسه ينطبق على النقطة B.

أنواع الاتصال

يأخذ الاتصال أشكالًا مختلفة في الطوبولوجيا، لكن الشكلين الأكثر شيوعًا هما:

• الاتصال الطوبولوجي
  يُقال إن الفضاء الطوبولوجي $ X $ هو متصل إذا كان من المستحيل تقسيمه إلى مجموعتين مفتوحتين غير فارغتين ومتباينتين يشكّل اتحادهما الفضاء بأكمله. وبعبارة أخرى، لا يمكن "فصل" الفضاء إلى منطقتين مستقلتين عن بعضهما البعض.

  مثال. الفضاء (-1, 1) متصل، في حين أن الفضاء (-1, 0) ∪ (0, 1) غير متصل، لأن هناك مجموعتين مفتوحتين غير فارغتين ومتباينتين هما (-1, 0) و(0, 1)، واتحادهما يشكّل الفضاء كله.
  وبالتالي، تُعدّ هاتان المجموعتان فصلًا للفضاء.

• الاتصال بالمسار (أو الاتصال بالقوس)
  يُقال إن الفضاء الطوبولوجي متصل بالمسار إذا أمكن لأي نقطتين A وB داخله إيجاد مسار مستمر يربط بينهما دون الخروج من الفضاء. وكل فضاء متصل بالمسار هو أيضًا متصل طوبولوجيًا، غير أن العكس ليس بالضرورة صحيحًا.

  على سبيل المثال، تخيّل شكلًا مغلقًا على سطح مستوٍ. لأي نقطتين داخليتين A وB، يمكن رسم منحنى مستمر يصل بينهما دون رفع القلم عن الورقة أو مغادرة حدود الشكل.
  
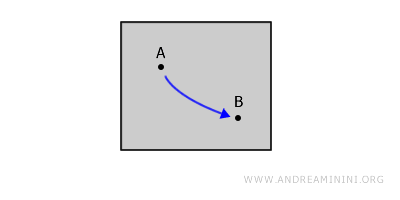
  الفرق بين الاتصال بالقوس والاتصال بالمسار:  الاتصال بالقوس يشبه الاتصال بالمسار، لكنه أكثر تحديدًا: يجب أن يكون المسار أحاديًا (واحدًا لواحد)، أي لا يمر بالنقطة نفسها أكثر من مرة ولا يتقاطع مع نفسه.

• الاتصال البسيط
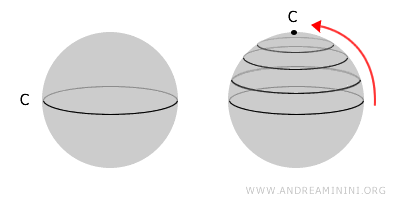
  يُقال إن الفضاء بسيط الاتصال إذا أمكن اختزال أي حلقة مغلقة داخله إلى نقطة واحدة من دون تمزيق أو خروج عن الفضاء. هذا يعني أن الفضاء لا يحتوي على ثقوب داخلية. كل فضاء بسيط الاتصال هو فضاء متصل، لكن ليس كل فضاء متصل بسيط الاتصال.

  فعلى سبيل المثال، الكرة تُعد فضاءً بسيط الاتصال لأن أي حلقة على سطحها يمكن اختزالها إلى نقطة. أما الطوروس (شكل الكعكة ذات الثقب) فيُظهر نوعًا مختلفًا من الاتصال، إذ لا يمكن تقليص جميع الحلقات إلى نقطة واحدة.
  
  
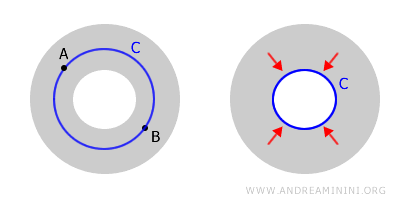
  هذا النوع من الفضاءات، المتصلة ولكن غير بسيطة الاتصال، يُعرف باسم الفضاءات متعددة الاتصال، ومن أمثلتها الحلقة أو الفضاء الحلقي.

ملاحظات ختامية

قبل أن نختتم، من المفيد تذكر هذه الملاحظة البسيطة:

• في مجموعة الأعداد الحقيقية، الفضاءات المتصلة الوحيدة هي الفترات.