الفضاءات المتصلة بالمسار

نقول إن الفضاء الطوبولوجي S هو فضاء متصل بالمسار إذا أمكن رسم مسار مستمر يربط بين أي نقطتين A وB داخله دون الخروج منه.

تخيّل أنك تنظر إلى ورقة مسطحة وتغض النظر عن حوافها.

هذه الورقة تمثل سطحاً واحداً متصلاً، وهي تُعتبر فضاءً مفتوحاً لأنها لا تضم الحدود.

إذا اخترت نقطتين A وB على الورقة، يمكنك ببساطة رسم خط بينهما دون رفع القلم عن الورقة.

بكلمات بسيطة، المسار يظل دائماً داخل الفضاء الذي يحتوي النقطتين A وB.

كل فضاء متصل بالمسار هو فضاء متصل، لأن وجود مسار بين كل نقطتين يعني أن الفضاء لا ينقسم إلى أجزاء منفصلة.

لكن العكس غير صحيح دائماً. ليس كل فضاء متصل هو فضاء متصل بالمسار.

قد يبدو هذا غير بديهي، لكنه مثال جميل على دقة المفاهيم الرياضية.

انظر إلى المثال التالي الذي يتضمن مجموعتين Q وT:

$$ Q = \{ \forall \ x \ \in R-\{ 0 \} \ , \ \sin( \frac{1}{x} ) \} $$

$$ T = \{ \ 0 \} $$

المجموعة الأولى Q تمثل جميع النقاط الواقعة على منحنى الدالة الجيبية sin(1/x)، وهي معرفة لكل عدد حقيقي ما عدا عند الصفر، لأن القسمة على صفر غير معرفة.

أما المجموعة الثانية T فتتكون فقط من النقطة 0.

المنحنى Q يقترب إلى ما لا نهاية من النقطة 0، لكنه لا يلمسها فعلاً. يمكن رؤية ذلك في الرسم التالي:

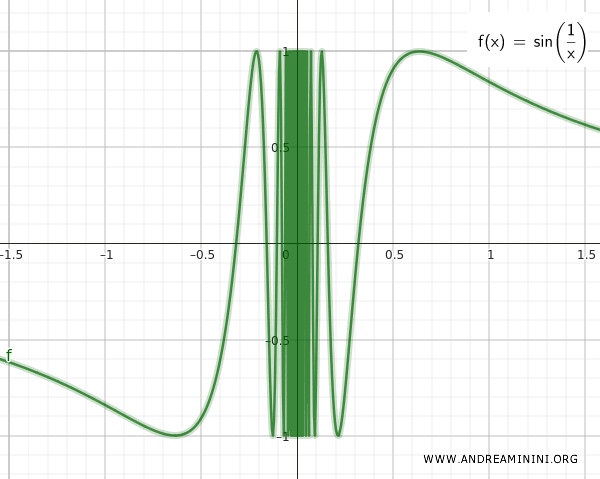
الفضاء الناتج S هو اتحاد المجموعتين Q وT:

$$ S = Q \cup T $$

الفضاء S متصل لأن النقطة 0 هي نقطة تراكم لمنحنى sin(1/x)، أي أنه في أي جوار صغير حول الصفر سنجد نقاطاً من Q.

ومع ذلك، فإن S ليس متصلاً بالمسار، لأننا لا نستطيع رسم أي مسار مستمر يربط بين نقطة من Q والنقطة 0 دون مغادرة الفضاء.

ملاحظة: لو كانت الدالة بدلاً من ذلك f(x)=1/x، لكانت المجموعتان Q وT منفصلتين تماماً ولا تقاربان بعضهما.

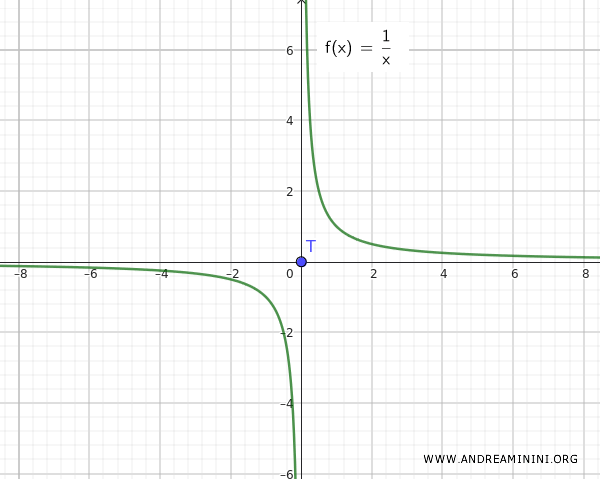
يُظهر هذا المثال أن اتحاد مجموعة متصلة Q={∀ x ∈ R-{0}, 1/x} مع نقطة معزولة T={0} لا يؤدي بالضرورة إلى فضاء متصل، ما لم تكن النقطة المعزولة (مثل الصفر) أيضاً نقطة تراكم.

 وهكذا نرى أن الاتصال بالمسار مفهوم أدق وأعمق من الاتصال فقط.