اتحاد الجزأين الداخليين لمجموعتين
يُعد اتحاد الجزأين الداخليين لمجموعتين \( A \) و\( B \) من الخصائص الأساسية في الطوبولوجيا. إذ يكون هذا الاتحاد دائمًا محتوى ضمن الجزء الداخلي لاتحاد المجموعتين: \[ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B) \] غير أن هذه العلاقة لا تعني بالضرورة تحقق المساواة.
توضح هذه الخاصية أن أخذ الأجزاء الداخلية أولًا ثم إجراء الاتحاد لا يمكن أن يولد نقاطًا جديدة خارج الجزء الداخلي لاتحاد المجموعتين.
ومع ذلك، لا تكون المجموعتان متساويتين في جميع الحالات. أي أنه لا يصح دائمًا أن:
$$ \text{Int}(A) \cup \text{Int}(B) = \text{Int}(A \cup B) $$
فقد يتحقق الاحتواء دون أن تتحقق المساواة:
$$ \text{Int}(A) \cup \text{Int}(B) \ne \text{Int}(A \cup B) $$
يساعد هذا الفرق على تكوين تصور أوضح لطبيعة العمليات الطوبولوجية وكيفية تفاعل المجموعات مع أجزائها الداخلية.
مثال توضيحي
لنأخذ مجالين مفتوحين \( A \) و\( B \) في مجموعة الأعداد الحقيقية \(\mathbb{R}\) مع الطوبولوجيا القياسية:
$$ A = (0, 2) $$
$$ B = (1, 3) $$
بما أن المجالين مفتوحان، فإن الجزء الداخلي لكل منهما هو المجال نفسه:
$$ \text{Int}(A) = (0, 2) $$
$$ \text{Int}(B) = (1, 3) $$
ومن ثم يكون اتحاد الجزأين الداخليين:
$$ \text{Int}(A) \cup \text{Int}(B) = (0, 2) \cup (1, 3) $$
وهذا الاتحاد يساوي المجال:
$$ (0, 3) $$
أما اتحاد المجالين أنفسهما فهو:
$$ A \cup B = (0, 3) $$
وبالتالي يكون الجزء الداخلي لاتحاد المجموعتين:
$$ \text{Int}(A \cup B) = (0, 3) $$
في هذه الحالة نلاحظ أن الاحتواء يتحقق، بل إن المساواة تتحقق أيضًا:
$$ \text{Int}(A) \cup \text{Int}(B) = \text{Int}(A \cup B) $$
لكن هذا ليس الوضع دائمًا.
على سبيل المثال، إذا اعتبرنا المجالين المغلقين: $$ A = [0, 2] $$ $$ B = [2, 3] $$ فإن الجزأين الداخليين هما: $$ \text{Int}(A) = (0, 2) $$ $$ \text{Int}(B) = (2, 3) $$ بينما اتحاد المجموعتين هو: $$ A \cup B = [0, 3] $$ ويكون جزؤه الداخلي: $$ \text{Int}(A \cup B) = (0, 3) $$ نلاحظ أن: $$ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B) $$ لكن المساواة لا تتحقق، لأن النقطة \(2\) تنتمي إلى الجزء الداخلي للاتحاد: $$ 2 \in \text{Int}(A \cup B) $$ ولا تنتمي إلى أي من الجزأين الداخليين: $$ 2 \notin \text{Int}(A), \quad 2 \notin \text{Int}(B) $$ ومن ثم: $$ \text{Int}(A) \cup \text{Int}(B) \ne \text{Int}(A \cup B) $$
المثال 2
لننظر الآن إلى مجالين مفتوحين غير متداخلين:
$$ A = (0, 1) $$
$$ B = (2, 3) $$
في هذه الحالة يكون:
$$ \text{Int}(A) = (0, 1) $$
$$ \text{Int}(B) = (2, 3) $$
ويكون اتحاد الجزأين الداخليين:
$$ \text{Int}(A) \cup \text{Int}(B) = (0, 1) \cup (2, 3) $$
كما أن الجزء الداخلي لاتحاد المجموعتين يساوي:
$$ \text{Int}(A \cup B) = (0, 1) \cup (2, 3) $$
وهنا تتحقق المساواة مرة أخرى.
المثال 3
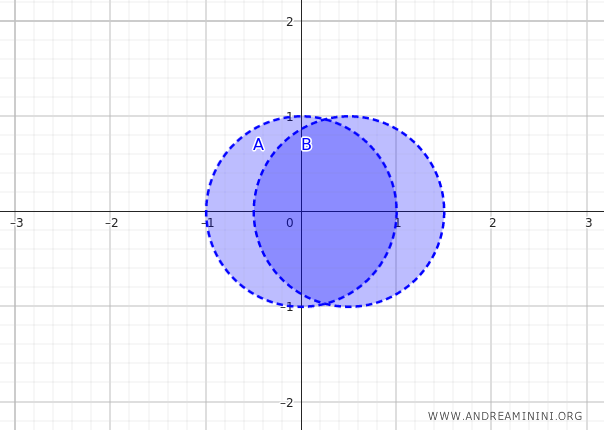
ننتقل الآن إلى مثال في المستوى الحقيقي \(\mathbb{R}^2\). لنعتبر مجموعتين \( A \) و\( B \) تمثلان قرصين مفتوحين متداخلين جزئيًا.
يُعطى القرصان بالعلاقتين:
$$ A = \{ (x,y) \in \mathbb{R}^2 \mid x^2 + y^2 < 1 \} $$
$$ B = \{ (x,y) \in \mathbb{R}^2 \mid (x-0.5)^2 + y^2 < 1 \} $$
وبما أن المجموعتين مفتوحتان، فإن:
$$ \text{Int}(A) = A $$
$$ \text{Int}(B) = B $$
ومن ثم:
$$ \text{Int}(A) \cup \text{Int}(B) = A \cup B $$
كما أن الجزء الداخلي لاتحاد المجموعتين يساوي الاتحاد نفسه:
$$ \text{Int}(A \cup B) = A \cup B $$
وهذا يؤكد مرة أخرى تحقق علاقة الاحتواء.
البرهان
لإثبات هذه الخاصية بصورة عامة، نبرهن أن:
$$ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B) $$
بحسب تعريف الجزء الداخلي، فإن النقطة \( x \) تنتمي إلى \( \text{Int}(X) \) إذا وُجد لها جوار مفتوح محتوى كليًا داخل المجموعة \( X \).
إذا كانت \( x \in \text{Int}(A) \cup \text{Int}(B) \)، فهذا يعني أن \( x \) تنتمي إلى الجزء الداخلي لإحدى المجموعتين على الأقل.
- إذا كانت \( x \in \text{Int}(A) \)، فهناك جوار مفتوح \( U_x \subseteq A \).
- إذا كانت \( x \in \text{Int}(B) \)، فهناك جوار مفتوح \( V_x \subseteq B \).
وفي كلتا الحالتين يكون هذا الجوار محتوى في \( A \cup B \)، ومن ثم تكون \( x \) نقطة داخلية في اتحاد المجموعتين.
وبذلك نستنتج أن كل نقطة في اتحاد الجزأين الداخليين هي نقطة داخلية في اتحاد المجموعتين، أي:
$$ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B) $$
وهذا ما يثبت الخاصية المطلوبة.