النقاط الثابتة في الطوبولوجيا

في الطوبولوجيا تُعرّف النقطة الثابتة بأنها قيمة لا تتغير عند تطبيق دالة عليها.

عند دراسة دالة مثل f(x)، نقول إن قيمة ما تُعد نقطة ثابتة إذا تحقّق الشرط f(p) = p. بمعنى آخر، في هذه الحالة يكون ناتج الدالة مساوياً تماماً لمدخلها عند النقطة p.

$$ f(p) = p $$

فكرة تمهيدية

تأمل جسماً يدور حول نقطة مركزية P. أثناء عملية الدوران تتغير إحداثيات جميع نقاط الجسم في الفضاء، باستثناء نقطة واحدة تبقى كما هي. هذه النقطة هي مركز الدوران، أي النقطة الثابتة التي لا يمسها تأثير الحركة.

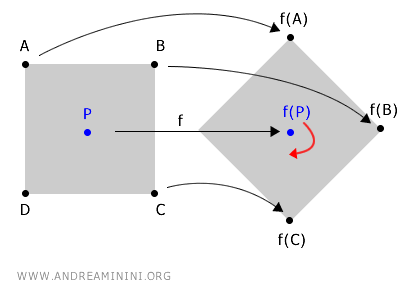
في هذا المثال تمثل النقطة P نقطة ثابتة، لأنها لا تتبدل عند تطبيق دالة الدوران عليها.

$$ f(P) \longrightarrow P $$

تظهر فكرة النقاط الثابتة في مجالات واسعة داخل الرياضيات وخارجها، مثل التحليل العددي ونظرية الألعاب والاقتصاد. وتساعد هذه الفكرة في فهم سلوك الأنظمة التي تسعى بطبيعتها إلى حالة توازن أو استقرار.

أمثلة توضيحية

لنبدأ بالدالة التالية على الفترة المغلقة ‎[0, 2π]:

$$ f(x) = \sin(x) $$

من السهل ملاحظة أن النقطة p = 0 تُعد نقطة ثابتة لأن:

$$ \sin(0) = 0 $$

في هذا المثال يتطابق الناتج مع المدخل بشكل مباشر.

مثال ثانٍ

لننتقل الآن إلى الدالة التالية على الفترة نفسها ‎[0, 2π]:

$$ f(x) = \cos(x) $$

نلاحظ هنا أن x = 0 ليست نقطة ثابتة لأن:

$$ \cos(0) = 1 $$

بدلاً من ذلك تمتلك الدالة نقطة ثابتة تقريبية تقع عند:

$$ x \approx 0.73908513 $$

إذ إن:

$$ \cos(0.73908513) \approx 0.73908513 $$

بهذا نكون أمام نقطة يتحقق عندها شرط التطابق بين المدخل والمخرج بدقة جيدة.

مبرهنة براور للنقطة الثابتة

تُعد مبرهنة براور من أهم نتائج الطوبولوجيا في هذا المجال، وتنص على ما يلي:

كل دالة مستمرة معرفة على مجموعة مغلقة ومحدودة في بعد n تمتلك نقطة ثابتة واحدة على الأقل.

تكمن أهمية هذه المبرهنة في كونها مبرهنة وجود، فهي تضمن أن نقطة ثابتة لا بد أن تكون موجودة، حتى لو لم نتمكن من تحديد موضعها بدقة.

تجد هذه الفكرة تطبيقات واسعة، خصوصاً في دراسة الأنظمة الديناميكية التي تسعى إلى حالة توازن، وكذلك في النماذج الاقتصادية التي تحاول التنبؤ بحالات الاستقرار في الأسواق أو السياسات المالية.

وتبقى النقاط الثابتة موضوعاً جذاباً للبحث والدراسة، لما توفره من أدوات قوية لفهم البنى الرياضية والسلوكيات المعقدة في النظم المختلفة.