طوبولوجيا المجموعات المفتوحة

بذلك تكون الطوبولوجيا T قائمة على مجموعات جزئية من X تُعدّ مفتوحة بطبيعتها، مع ضمان ثباتها تحت عمليتي الاجتماع والتقاطع. وتسمى عائلة المجموعات مجموعة يحتوي كل عنصر فيها على مجموعة أو مجموعة جزئية.

عندما تجتمع X مع الطوبولوجيا T تتكوّن بنية تُسمّى فضاءً طوبولوجياً يُرمز إليه بالزوج (X,T). من الشائع اختصار العبارة بالقول إن X فضاء طوبولوجي، لكن في الحقيقة الفضاء يتكوّن من عنصرين: المجموعة X والطوبولوجيا T التي تحدد المجموعات المفتوحة داخلها.

لماذا تُعدّ المجموعة الخالية مفتوحة؟

وفق التعريف الطوبولوجي، تُصنف المجموعة الخالية كمجموعة مفتوحة في كل فضاء طوبولوجي. وجود هذا الشرط ليس تفصيلاً ثانوياً، بل يضمن انسجام القواعد وبقاء النظام الداخلي للطوبولوجيا كاملاً ومنسجماً.

مثال تطبيقي

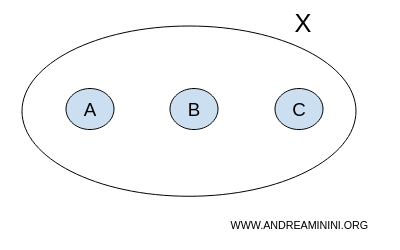
لنفترض أن لدينا مجموعة بسيطة:

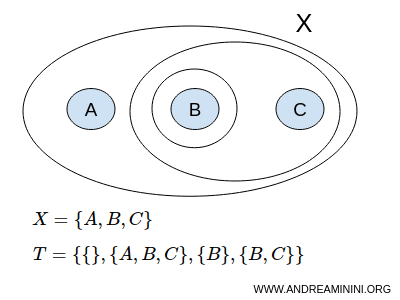
$$ X = \{ A,B,C \} $$

ولنعرّف طوبولوجيا T على هذه المجموعة بالشكل الآتي:

$$ T = \{ \{ \},\{A,B,C \}, \{ B \}, \{ B,C \}  \} $$

تمثل { } المجموعة الخالية Ø، وتمثل {A,B,C} المجموعة الكاملة X. وبموجب التعريف، تكون كل منهما مجموعة مفتوحة.

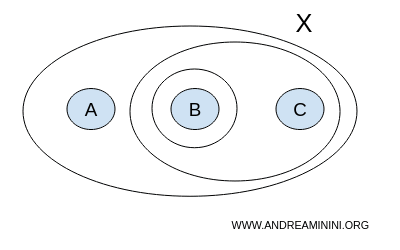
في هذه الحالة، إذا أجرينا اجتماعات أو تقاطعات لأي مجموعات جزئية داخل T فسنجد أنها تبقى ضمن العائلة نفسها. هذا يعني أن T مغلقة تحت عمليتي الاجتماع والتقاطع، وبالتالي فهي طوبولوجيا صحيحة على X.

مثال آخر

لنستخدم المجموعة نفسها:

$$ X = \{ A,B,C \} $$

ولكن هذه المرة نضيف المجموعة {A} إلى العائلة:

$$ T = \{ \{ \},\{A,B,C \}, \{ A \}, \{ B \}, \{ B,C \}  \} $$

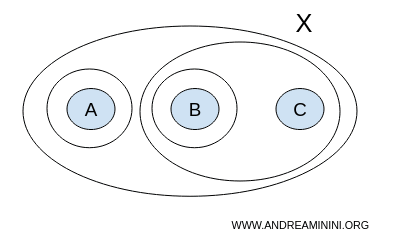
قد تبدو هذه العائلة مناسبة للوهلة الأولى، لكنها ليست طوبولوجيا. فالاجتماع بين {A} و{B} ينتج المجموعة {A,B}، وهي غير موجودة ضمن عناصر T. وبذلك تفشل العائلة في تحقيق أحد شروط تعريف الطوبولوجيا، وهو الثبات تحت عملية الاجتماع.

النتيجة هي أن هذه العائلة لا يمكن اعتبارها طوبولوجيا على X.

خلاصة

الطوبولوجيا إطار رياضي يحدد شكل المجموعات المفتوحة داخل أي مجموعة، ويُعدّ أساساً للعديد من الفروع المتقدمة في الرياضيات. يكفي لاستيعاب فكرتها إدراك شرطين اثنين: احتواء المجموعة الخالية والمجموعة الأصلية، والثبات تحت الاجتماع والتقاطع. ومع الأمثلة البسيطة يمكن تكوين فهم متين يمهّد لاكتشاف تطبيقات أعمق في مجالات التحليل والدوال والفضاءات المجردة.