طوبولوجيا الفضاء الفرعي

عندما نتعامل مع فضاء طوبولوجي \( (X, T) \)، حيث تمثل \( T \) عائلة المجموعات المفتوحة التي تحدد بنية الفضاء، ويكون \( Y \) فضاءً فرعياً من \( X \)، فإن طوبولوجيا الفضاء الفرعي تُعرّف ببساطة باعتبار المجموعات المفتوحة في \( Y \) هي تلك الناتجة من تقاطع \( Y \) مع المجموعات المفتوحة في \( X \). الصيغة الأساسية لهذه الفكرة هي: \[
T_Y = \{ U \cap Y \mid U \in T \}. \] وهذه الطوبولوجيا تُعرف أيضاً باسم الطوبولوجيا المستحثّة.

وبعبارة واضحة، تكون المجموعة \( V \subseteq Y \) مفتوحة في الفضاء الفرعي إذا أمكن الحصول عليها من مجموعة مفتوحة في \( X \) بعملية التقاطع معها. هذا يعني أن طبيعة openness في \( Y \) ترتبط مباشرة بالبنية الأصلية للفضاء \( X \).

$$ V_{open \ in \ Y} = U \cap Y $$

وينطبق المبدأ نفسه على المجموعات المغلقة. فكل مجموعة مغلقة في \( Y \) يمكن كتابتها بصيغة تقاطع مجموعة مغلقة في \( X \) مع \( Y \):

$$ V_{closed \ in \ Y} = C \cap Y $$

وبذلك يظهر الفضاء الفرعي على أنه فضاء يستمد خصائصه الطوبولوجية من الفضاء الأم، مع الحفاظ على بنيته الخاصة الناتجة عن عملية التقاطع.

ملاحظة. ليست جميع المجموعات المفتوحة في الفضاء الفرعي مفتوحة في الفضاء الأصلي، والعكس صحيح. فقد نجد مجموعات مفتوحة في \( Y \) مغلقة في \( X \)، أو مجموعات مفتوحة في الفضاءين معاً. كما توجد مجموعات تجمع بين الصفتين في آن واحد، وتسمى مجموعات مغلقة مفتوحة.

مثال تطبيقي

لفهم المفهوم بطريقة مباشرة، لنأخذ الفضاء الحقيقي \( \mathbb{R} \) مع طوبولوجيته المعيارية، حيث تشكل الفترات المفتوحة النموذج الأساسي للمجموعات المفتوحة.

ولنعتبر الفضاء الفرعي \( Y = [0, 1] \).

في هذه الحالة، تتكون طوبولوجيا الفضاء الفرعي من جميع المجموعات التي تأخذ الشكل:

$$ U \cap [0, 1] $$

حيث \( U \) مجموعة مفتوحة في \( \mathbb{R} \). فلو أخذنا الفترة المفتوحة (-1, 0.5) مثلاً، فإنها مفتوحة في \( \mathbb{R} \).

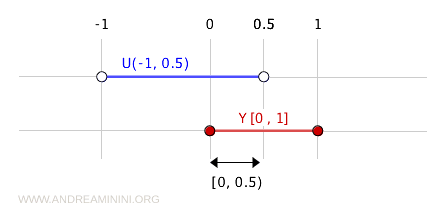
عند تقاطعها مع \( Y \) نحصل على:

$$ (-1, 0.5) \cap [0, 1] = [0, 0.5) $$

وهي مجموعة مفتوحة في الفضاء الفرعي \( Y \)، على الرغم من أنها ليست مفتوحة في الطوبولوجيا الأصلية على \( \mathbb{R} \).

أما الفترة \( [0, 0.5] \) فهي مغلقة في الفضاء الفرعي لأنها ناتجة من تقاطع الفترة المغلقة [-1, 0.5] مع \( Y \):

$$ [-1, 0.5] \cap [0, 1] = [0, 0.5] $$

ويتضح من هذا المثال أن الفضاء الفرعي يرث بنيته الطوبولوجية من الفضاء الأصلي بطريقة منهجية ودقيقة.

ملاحظة. بعض الفواصل مثل [0,a) أو (a,1] تعد مغلقة في الطوبولوجيا الأصلية، لكنها تصبح مفتوحة في الفضاء الفرعي لأنها تمثل تقاطع الفترة المفتوحة المناسبة في \( \mathbb{R} \) مع الفضاء الفرعي. ومثال ذلك: $$ (-1,0.5) \cap [0,1] = [0,0.5). $$ هذه المجموعة مفتوحة في \( Y \) رغم أنها ليست كذلك في \( X \).

كما توجد مجموعات تظل مفتوحة في الفضاءين، مثل الفترة (0.2, 0.8)، وأخرى تبقى مغلقة في الفضاءين مثل الفترة [0.2, 0.8].

وفي الفضاء الفرعي \( Y = [0, 1] \)، تظهر حالة لافتة هي أن الفترة \( [0, 1] \) مفتوحة ومغلقة في الوقت نفسه وفق الطوبولوجيا المستحثّة، لأنها تقاطع الفضاء مع نفسه.

• مفتوحة
  يثبت انفتاح \( [0, 1] \) في الفضاء الفرعي من خلال اختيار مجموعة مفتوحة \( U \subseteq \mathbb{R} \) تحقق $$ U \cap Y = [0, 1]. $$ وبما أن \( \mathbb{R} \) نفسه مجموعة مفتوحة في طوبولوجيته، نحصل مباشرة على: $$ \mathbb{R} \cap [0, 1] = [0, 1]. $$
• مغلقة
  أما إغلاق \( [0, 1] \) فيثبت باختيار مجموعة مغلقة \( C \subseteq \mathbb{R} \) تحقق $$ C \cap Y = [0, 1]. $$ والاختيار الطبيعي هو: $$ [0, 1] \cap [0, 1] = [0, 1]. $$

  ملاحظة: يمكن الاستفادة أيضاً من أن متمم \( [0, 1] \) في الفضاء الفرعي هو المجموعة الخالية، وهي مجموعة مفتوحة في أي طوبولوجيا، مما يعني أن \( [0, 1] \) مغلقة في الطوبولوجيا المستحثّة.

من هذا نستنتج أن الفترة \( [0, 1] \) مثال نموذجي لمجموعة تكون مفتوحة ومغلقة معاً في طوبولوجيا الفضاء الفرعي، وهي ما يسمى مجموعة مغلقة مفتوحة. تظهر مثل هذه الحالات في العديد من الفضاءات الطوبولوجية، وتمثل جانباً مهماً في فهم البنى الموروثة.

المثال 2

يساعدنا هذا المثال على فهم الطوبولوجيا المستحثّة بطريقة عملية. نبدأ بالفضاء \(\mathbb{R}\) المزوّد بالطوبولوجيا المعيارية، حيث تُعد الفترات المفتوحة (a,b) النموذج الأساسي للمجموعات المفتوحة.

الفضاء الفرعي الذي نهتم به هنا هو مجموعة الأعداد الصحيحة \(\mathbb{Z}\). ما يميز هذا الفضاء هو أن كل عدد صحيح يمكن عزله عن بقية الأعداد بتقاطع فترة مفتوحة من \(\mathbb{R}\) مع \(\mathbb{Z}\). هذه الفكرة البسيطة تجعل \(\mathbb{Z}\) مثالاً واضحاً لفضاء فرعي يحمل طوبولوجيا منفصلة مستمدة بالكامل من الفضاء الحقيقي.

على سبيل المثال، يمكن تحديد العدد 7 عن طريق تقاطع الفترة المفتوحة (6.5,7.5) مع \(\mathbb{Z}\):

$$ (6.5,7.5) \cap \mathbb{Z} = \{ 7 \} $$

وما دام هذا ممكناً لكل عدد صحيح، فإن كل عنصر في \(\mathbb{Z}\) يشكّل مجموعة مفتوحة في الطوبولوجيا المستحثّة. وبما أن المجموعات المفردة مفتوحة، فإن أي مجموعة جزئية من \(\mathbb{Z}\) تصبح بدورها مجموعة مفتوحة.

مثال آخر يوضح ذلك هو المجموعة {6,7,8} التي نحصل عليها عبر التقاطع التالي:

$$ (5.5,8.5) \cap \mathbb{Z} = \{ 6, 7, 8 \} $$

والنتيجة المهمة هنا هي أن الطوبولوجيا المستحثّة على \(\mathbb{Z}\) تتطابق تماماً مع الطوبولوجيا المنفصلة، حيث تكون جميع المجموعات مفتوحة دون استثناء.

ملاحظة: الطوبولوجيا المنفصلة على \(\mathbb{Z}\) ليست تعريفاً إضافياً، بل تظهر تلقائياً عندما نأخذ الطوبولوجيا المستحثّة من \(\mathbb{R}\). وهذا يمنحنا مثالاً تطبيقياً يُظهر كيف يمكن لطوبولوجيا فضاء كبير أن تنتج طوبولوجيا بسيطة للغاية عند حصرها في فضاء فرعي.

المثال 3

ننتقل الآن إلى مثال هندسي يوضح كيف تعمل الطوبولوجيا المستحثّة في فضاء أكثر تعقيداً. نبدأ بالفضاء الإقليدي الثلاثي الأبعاد \(\mathbb{R}^3\)، المزوّد بطوبولوجيته المعيارية القائمة على الكرات المفتوحة.

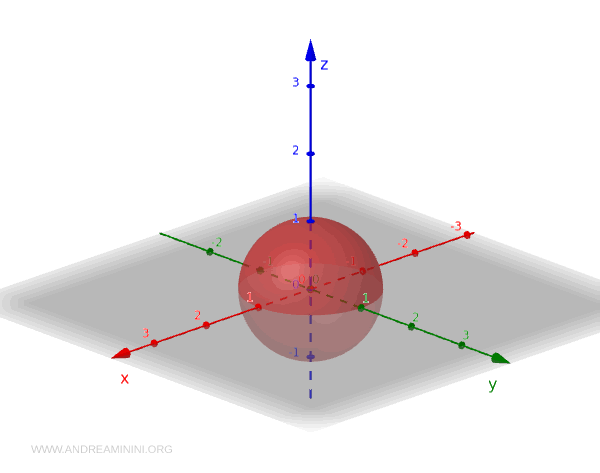
الفضاء الفرعي الذي ندرسه هنا هو الكرة الواحدة \( S^2 \)، أي مجموعة النقاط التي تبعد مسافة 1 عن الأصل:

$$ S^2 = \{ (x, y, z) \in \mathbb{R}^3 \mid x^2 + y^2 + z^2 = 1 \} $$

وتُعرّف الطوبولوجيا المستحثّة على \( S^2 \) عبر جميع المجموعات الناتجة من تقاطع \( S^2 \) مع مجموعات مفتوحة في \(\mathbb{R}^3\):

$$ T_{S^2} = \{ U \cap S^2 \mid U \text{ مفتوحة في } \mathbb{R}^3 \} $$

أي أن المجموعة \( V \subseteq S^2 \) تعد مفتوحة إذا كانت ناتجة من تقاطع \( S^2 \) مع مجموعة مفتوحة في الفضاء الأم.

لفهم هذه البنية بشكل أفضل، نستعرض بعض الأمثلة:

• الكرة كاملة كمجموعة مفتوحة
  إذا أخذنا المجموعة المفتوحة $$ U = \{ (x, y, z) \mid x^2 + y^2 + z^2 < 2 \}, $$ فإن كل نقطة في \( S^2 \) تحقق هذا الشرط، وبالتالي يكون $$ U \cap S^2 = S^2. $$ وهذا يعني أن \( S^2 \) مفتوحة في طوبولوجيتها المستحثّة.
• نصف الكرة العلوي
  نأخذ المجموعة $$ U = \{ (x, y, z) \mid x^2 + y^2 + z^2 = 1 \text{ و } z > 0 \}. $$ وهذا يحدد نصف الكرة العلوي. عند التقاطع نحصل على: $$ \{ (x, y, z) \in S^2 \mid z > 0 \}, $$ وهي مجموعة مفتوحة في الطوبولوجيا المستحثّة.
• قواعد عامة
  المجموعة الخالية \( \emptyset \) والفضاء نفسه \( S^2 \) مفتوحتان دائماً. كما أن تقاطع عدد منتهٍ من المجموعات المفتوحة يبقى مفتوحاً، والاتحاد الاعتباطي لمجموعات مفتوحة يبقى مفتوحاً أيضاً.

يتضح من ذلك أن \( S^2 \) يرث بنيته الطوبولوجية من الفضاء الأم بطريقة دقيقة وواضحة، حيث تُعرّف مجموعاته المفتوحة عبر التقاطع مع مجموعات مفتوحة في \(\mathbb{R}^3\).

خصائص طوبولوجيا الفضاء الفرعي

تتميز الطوبولوجيا المستحثّة بعدد من الخصائص المهمة التي تساعد على فهم بنيتها:

1. المجموعات المفتوحة
   كل مجموعة مفتوحة في \( Y \) تكون من الشكل \( U \cap Y \)، حيث \( U \) مفتوحة في \( X \).
2. المجموعة الخالية ومجموعة الفضاء
   الخالية \( \emptyset \) و\( Y \) نفسه مفتوحتان دائماً، لأنها ناتجة من تقاطع \( Y \) مع مجموعات مفتوحة في \( X \).
3. التقاطعات المنتهية
   تقاطع أي عدد منتهٍ من المجموعات المفتوحة في \( Y \) يبقى مفتوحاً، لأنه يمكن كتابته كتقاطع مجموعة مفتوحة في \( X \) مع \( Y \).
4. الاتحادات الاعتباطية
   الاتحاد الاعتباطي لمجموعات مفتوحة في \( Y \) يبقى مفتوحاً دائماً، لأنه يماثل اتحاد مجموعات مفتوحة في \( X \) ثم تقاطعها مع \( Y \).

ملاحظات

بعض الملاحظات المفيدة التي تساعد على تعميق الفهم:

• الطوبولوجيا المعيارية على أي فضاء فرعي من \(\mathbb{R}^n\) تتوافق تماماً مع الطوبولوجيا المستحثّة من طوبولوجيا \(\mathbb{R}^n\).

  مثال. إذا أخذنا \( Y = [-1,0) \cup (0,1] \)، فإن الفترتين [-1,0) و(0,1] مفتوحتان في \( Y \) لأنهما تنتجان من تقاطع \( Y \) مع فترتين مفتوحتين في \(\mathbb{R}\). كما أنهما مغلقتان أيضاً، لأن متمم كل منهما داخل \( Y \) هو الأخرى. وهكذا تكونان مجموعتين مغلقتين مفتوحتين في الوقت نفسه.

• مبرهنة الأساس في طوبولوجيا الفضاء الفرعي
  تنص هذه المبرهنة على أنه إذا كان \( B_X \) أساساً لطوبولوجيا الفضاء \( X \)، فإن $$ B_Y = \{ B \cap Y \mid B \in B_X \} $$ يشكّل أساساً للطوبولوجيا المستحثّة على \( Y \).

بهذا تتضح الصورة الكاملة للطوبولوجيا المستحثّة وكيف تنتقل من الفضاءات الأصلية إلى الفضاءات الفرعية، لتشكّل أداة مركزية في دراسة البنية الطوبولوجية وبناء الأمثلة النظرية والتطبيقية.