الطوبولوجيا

الطوبولوجيا فرع من فروع الرياضيات يهتم بدراسة الخصائص البنيوية للفضاءات، أي تلك الخصائص التي تبقى ثابتة تحت التحويلات المستمرة مثل التمديد أو الانحناء أو الالتواء، ما دام الجسم لا يتعرض للتمزيق أو اللصق.

ومن هذا المنطلق، تركز الطوبولوجيا على الخصائص الهندسية التي تُحفَظ كلما كان التحويل مستمرا وسلسا.

ولا يمكن لهذه الخصائص أن تتغير إلا عبر عمليات غير مستمرة، كتمزيق جزء من الفضاء أو لصق جزأين منه معا.

فعلى سبيل المثال، تُعد الكرة والمكعب متكافئين طوبولوجيا، إذ يمكن تشويه أحدهما تشويها مستمرا إلى الآخر دون أي تمزيق أو لصق.

أما الكرة والطارة، فليستا متكافئتين طوبولوجيا، لأن تحويل إحداهما إلى الأخرى يتطلب إنشاء ثقب أو إزالته، وهو ما يستلزم بالضرورة التمزيق أو اللصق.

وبعبارة مبسطة، تهتم الطوبولوجيا بكيفية تنظيم الفضاءات وترابط أجزائها، لا بالقياسات الدقيقة مثل المسافة أو الحجم أو الشكل.

ففي الإطار الطوبولوجي، لا يكون لمفاهيم مثل الطول أو المساحة أو الحجم أو قياس الزوايا أي دور أساسي. بل ينصب الاهتمام على الخصائص النوعية للأشكال، وعلى إمكانية تحويلها بعضها إلى بعض عبر تشوهات مستمرة.

ويشمل هذا المنظور، على سبيل المثال، مفهوم الاتصال، والتراص، وعدد الثقوب في الجسم، إضافة إلى خصائص كلية أخرى تميز الفضاء ككل.

كما تُدخل الطوبولوجيا مفهوم الفضاء الطوبولوجي، وتُعد التشاكلات الطوبولوجية أدواتها التحويلية الأساسية، وهي تطبيقات مستمرة وقابلة للعكس تسمح بتشويه الفضاء مع الحفاظ على بنيته الطوبولوجية.

ولهذا السبب، كثيرا ما تُوصَف الطوبولوجيا بأنها “هندسة الصفائح المطاطية”، حيث تُتصوَّر الأجسام وكأنها مصنوعة من مادة مرنة يمكن تمديدها أو ثنيها أو ضغطها، دون تمزيقها أو لصقها. وبفضل هذا المنظور، تُعد الطوبولوجيا من أكثر فروع الرياضيات الحديثة عمقا وقدرة على الربط بين مجالات مختلفة.

لمحة تاريخية

تبدأ قصة الطوبولوجيا في القرن الثامن عشر، عندما طرح ليونهارد أويلر واحدة من أشهر المسائل في تاريخ الرياضيات: مسألة الجسور السبعة في كونيغسبرغ.

في تلك المدينة، كانت هناك سبعة جسور تربط بين ضفتي النهر. تساءل أويلر: هل يمكن عبور كل الجسور مرة واحدة فقط دون تكرار أي منها؟

مسألة الجسور السبعة:

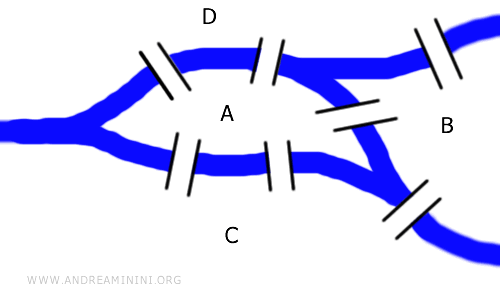
هذه المسألة لا تحتاج إلى معرفة أطوال الجسور أو المسافات بينها. ما يهم هو طريقة اتصالها فقط. ولهذا السبب تُعتبر أول مسألة طوبولوجية في التاريخ، إذ يمكن تمثيلها أيضاً بالرسم البياني الموضّح هنا:

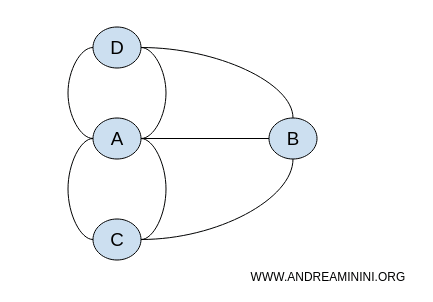
في هذا التمثيل، لا يهم موقع النقاط بدقة، بل العلاقات التي تربطها ببعضها. أي عدد من الرسوم المختلفة يمكن أن يكون مكافئاً من الناحية الطوبولوجية طالما يحافظ على نفس نمط الاتصال.

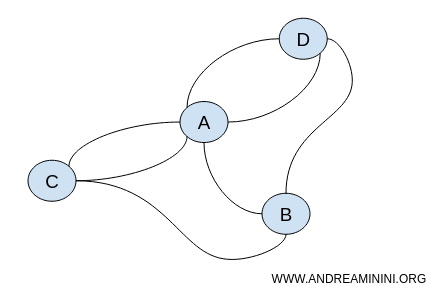
كلا الرسمين أعلاه يعبّران عن النظام نفسه رغم اختلاف الشكل. هذا هو جوهر التفكير الطوبولوجي.

من خلال هذه المسألة، بيّن أويلر أن ما يهم ليس القياس بل العلاقات المكانية. وهكذا وُلدت فكرة «هندسة الموضع»، التي ستتطور لاحقاً إلى ما نعرفه اليوم باسم الطوبولوجيا.

في القرن التاسع عشر، تابع علماء كبار مثل غاوس وموبيوس وريمان وكلاين دراسة خصائص الأسطح والأشكال، مما مهد الطريق لقيام الطوبولوجيا كفرع مستقل.

معلومة: كان يوهان ليستنغ أول من استخدم مصطلح «الطوبولوجيا» عام 1847، لكن الفكرة لم تنتشر إلا بعد عقود بفضل أعمال بوانكاريه في الطوبولوجيا الجبرية.

الفضاءات الطوبولوجية

الفضاء الطوبولوجي هو ببساطة مجموعة من النقاط مرفقة بنظام يحدد أي المجموعات منها تُعتبر «مفتوحة». هذا الإطار يسمح بدراسة مفاهيم مثل الاستمرارية والتقارب بطريقة عامة وشاملة.

$$ (X,T) $$

مثال: خط الأعداد الحقيقي \( \mathbb{R} \) مع طوبولوجيته القياسية هو المثال الأشهر. المجموعة تُعد مفتوحة إذا احتوت على فترة حول كل نقطة فيها. بهذه الفكرة يمكننا فهم الاستمرارية والحدود دون الحاجة إلى قياسات محددة.

التطابق الطوبولوجي

التطابق الطوبولوجي (Homeomorphism) هو نوع خاص من التحويلات الرياضية التي تربط بين فضاءين بطريقة تحافظ على جوهر بنيتهما. أي يمكننا الانتقال من أحدهما إلى الآخر عبر تحوّل مستمر، والعكس بالعكس.

إذا وُجد مثل هذا التحويل بين فضاءين، نقول إنهما متكافئان طوبولوجياً.

مثال: تخيّل فنجان قهوة وكعكة دونات - قد يبدوان مختلفين، لكن كليهما يحتوي على فتحة واحدة. يمكن تحويل أحدهما إلى الآخر عبر تشوه مستمر دون تمزيق أو لصق.

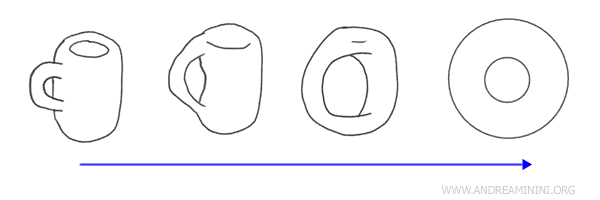
الفرق بين الهندسة والطوبولوجيا

قد تبدو الهندسة والطوبولوجيا متشابهتين، لكنهما تنظران إلى العالم من زاويتين مختلفتين تماماً:

• الهندسة تدرس المسافات والزوايا والقياسات الدقيقة. إنها تهتم بالشكل كما نراه بالعين المجردة.
  

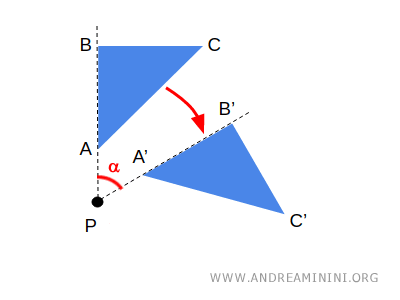
  الهندسة الإقليدية هي الأشهر، لكن هناك أيضاً هندسات غير إقليدية تدرس عوالم مختلفة حيث قوانين المسافة ليست نفسها.

• الطوبولوجيا تركز على جوهر الأشكال الذي يبقى ثابتاً رغم التغيرات المستمرة. ما يهمها هو الاتصال، والمرونة، والعلاقات بين الأجزاء. إذا ضغطت مكعباً من الطين ليصبح كرة دون أن تضيف أو تزيل مادة، فأنت لم تغيّر طبيعته الطوبولوجية.
  

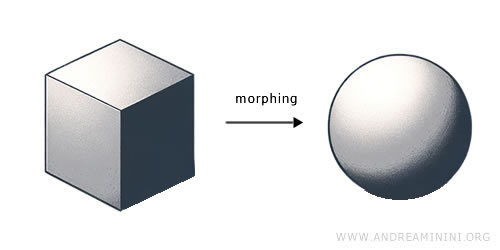
  مثال: مكعب الطين يمكن ضغطه ليصبح كرة دون فقدان الاتصال أو الاستمرارية. هذا ما يسميه الرياضيون «تطابقاً طوبولوجياً».
  

لهذا السبب يُقال إن الطوبولوجيا هي «تعميم للهندسة»، لأنها تنظر إلى ما وراء القياسات لتكتشف العلاقات العميقة بين الأشكال.

فروع الطوبولوجيا الحديثة

مع توسّع هذا المجال، ظهرت فروع متعددة للطوبولوجيا، لكل منها أدواته الخاصة وتطبيقاته المميزة:

• الطوبولوجيا الهندسية: تدرس الأشكال التي يمكن تحويلها بعضها إلى بعض من دون تمزيق أو لصق، مع التركيز على خصائص مثل الاتصال والدمج والحدود.
• الطوبولوجيا العامة: وتُعرف أيضاً باسم طوبولوجيا المجموعات النقطية، وتتعامل مع المفاهيم الأساسية مثل المجموعات المفتوحة والمغلقة، والاستمرارية، والدمج، والاتصال، وفضاءات الدوال.
• الطوبولوجيا الجبرية: تستخدم أدوات الجبر لفهم الفضاءات الطوبولوجية عبر تحويلها إلى رموز ومعادلات تمكّن من تحليلها بدقة.
• الطوبولوجيا التفاضلية: تدمج بين الطوبولوجيا وحساب التفاضل لدراسة الأسطح الملساء والخصائص المحلية للأشكال القابلة للاشتقاق.
• الطوبولوجيا التطبيقية: تُستخدم في مجالات حديثة مثل تحليل البيانات، وهندسة الشبكات، والذكاء الاصطناعي، والبيولوجيا الرياضية.

بفضل هذه الفروع، لم تعد الطوبولوجيا علماً تجريدياً فقط، بل أصبحت أداة قوية لفهم الأنظمة المعقدة في الرياضيات والعلوم والهندسة على حد سواء.

إن الطوبولوجيا لا تكتفي بدراسة الأشكال، بل تفتح نافذة لفهم الترابط الخفي بين الأشياء - من الجسور القديمة إلى شبكات الإنترنت الحديثة.