تقاطع داخل مجموعتين

تقاطع داخل مجموعتين $A$ و$B$ يساوي داخل تقاطعهما $ \text{Int}(A \cap B) $ $$ \text{Int}(A) \cap \text{Int}(B) = \text{Int}(A \cap B) $$

تعبر هذه النتيجة عن خاصية أساسية في الطوبولوجيا، مفادها أن تقاطع داخل مجموعتين لا يختلف عن داخل المجموعة الناتجة عن تقاطعهما.

بصيغة مباشرة، إذا نظرنا إلى جميع النقاط الواقعة داخل $A$ وجميع النقاط الواقعة داخل $B$، ثم أخذنا النقاط المشتركة بين هاتين المجموعتين، فإننا نحصل تمامًا على النقاط التي تشكّل داخل المجموعة $A \cap B$.

لفهم هذه الفكرة بوضوح، من المفيد التوقف عند مفهومين أساسيين:

داخل مجموعة ($\text{Int}(A)$): هو مجموعة جميع النقاط التابعة للمجموعة $A$ والتي لا تقع على حدودها. وتمتاز كل نقطة داخلية بوجود جوار مفتوح حولها يكون محتوى كليًا داخل $A$.
التقاطع ($\cap$): هو مجموعة جميع النقاط التي تنتمي في الوقت نفسه إلى كل من المجموعتين $A$ و$B$.

وبالتالي، فإن أخذ تقاطع داخل $A$ مع داخل $B$ يؤدي مباشرة إلى داخل المجموعة المشتركة $A \cap B$.

مثال تطبيقي
البرهان

مثال تطبيقي

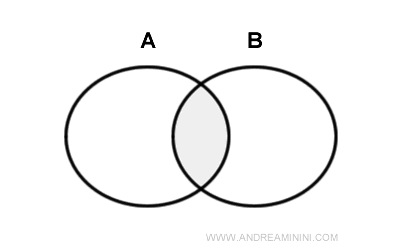
لنتخيّل دائرتين $A$ و$B$ تتداخلان جزئيًا.

يمثل داخل كل دائرة المساحة الكاملة باستثناء محيطها. وعند النظر إلى المنطقتين الداخليتين معًا، نجد أن الجزء المشترك بينهما يمثل بالضبط داخل المنطقة التي يتقاطع فيها $A$ و$B$.

تقاطع المجموعات

البرهان

يعتمد البرهان على إثبات احتواءين متعاكسين، وهو أسلوب شائع في إثبات تساوي مجموعتين في الرياضيات.

1] الاحتواء الأول ($\subseteq$)

إذا كانت نقطة ما داخل $A$ وداخل $B$ في آن واحد، فإنها محاطة بجوار مفتوح يقع كليًا داخل كلتا المجموعتين. وبما أن هذا الجوار مشترك بينهما، فهو يقع داخل $A \cap B$، ما يعني أن النقطة تنتمي إلى داخل هذا التقاطع.

لتكن $x \in \text{Int}(A) \cap \text{Int}(B)$. عندئذٍ يكون $x \in \text{Int}(A)$ و$x \in \text{Int}(B)$.

وبحسب تعريف الداخل، يوجد جواران مفتوحان $U$ و$V$ بحيث $x \in U \subseteq A$ و$x \in V \subseteq B$.

نأخذ الجوار $W = U \cap V$. وبما أن $U$ و$V$ مفتوحان، فإن $W$ مفتوح أيضًا ويحتوي النقطة $x$.

كما أن $W \subseteq A \cap B$، ومن ثمّ $x \in \text{Int}(A \cap B)$.

وعليه، $\text{Int}(A) \cap \text{Int}(B) \subseteq \text{Int}(A \cap B)$.

2] الاحتواء الثاني ($\supseteq$)

أما إذا كانت النقطة داخل $A \cap B$، فهذا يعني وجود جوار مفتوح حولها يقع كليًا داخل هذا التقاطع. وبما أن التقاطع محتوى في كل من $A$ و$B$، فإن هذه النقطة تكون داخل كلتا المجموعتين.

لتكن $x \in \text{Int}(A \cap B)$. عندئذٍ يوجد جوار مفتوح $W$ للنقطة $x$ بحيث $W \subseteq A \cap B$.

وبما أن $W \subseteq A \cap B$، فإن $W \subseteq A$ و$W \subseteq B$.

وعليه، $x \in \text{Int}(A)$ و$x \in \text{Int}(B)$.

ومن ثمّ، $\text{Int}(A \cap B) \subseteq \text{Int}(A) \cap \text{Int}(B)$.

وبإثبات الاحتواءين معًا، نستنتج أن:

\[ \text{Int}(A) \cap \text{Int}(B) = \text{Int}(A \cap B) \]

وبذلك يكتمل البرهان بصورة واضحة ومباشرة.