الفضاء التبولوجي الطبيعي

يُقال إن الفضاء التبولوجي $ X $ فضاء طبيعي إذا تحقق فيه الشرطان الآتيان:

كل مجموعة أحادية العنصر مغلقة
أي أن كل نقطة $ x \in X $ تكون مجموعتها الأحادية $\{x\}$ مغلقة في الطوبولوجيا المعطاة.
إمكانية فصل أي مجموعتين مغلقتين منفصلتين بواسطة مجموعتين مفتوحتين منفصلتين
فإذا كانت $ A $ و $ B $ مجموعتين مغلقتين لا تتقاطعان، أي $ A \cap B = \emptyset $، فإنه توجد مجموعتان مفتوحتان $ U $ و $ V $ تحققان:
- $ A \subset U $
- $ B \subset V $
- $ U \cap V = \emptyset $.

تعبر خاصية الطبيعية عن قدرة الفضاء على احتواء مجموعتين مغلقتين منفصلتين داخل جوارين مفتوحين منفصلين تماماً. وبصيغة أخرى، عندما تكون لدينا مجموعتان مغلقتان لا تتقاطعان، يمكن دائماً إيجاد جوارين مفتوحين لا يلتقيان يحتوي كل منهما إحدى المجموعتين.

وتُعد هذه الخاصية ركناً أساسياً في تشييد دوال مستمرة تميز بين النقاط أو بين المجموعات المغلقة.

مثال عملي
ملاحظات إضافية

مثال عملي

لننظر إلى الفضاء $ X = \mathbb{R} $ المزود بالطوبولوجيا القياسية المتولدة عن الفواصل المفتوحة $ (a, b) $.

نأخذ مثالاً لمجموعتين مغلقتين منفصلتين في $ \mathbb{R} $:

$ A = \{0\} $، وهي مجموعة أحادية العنصر.
$ B = [2, 3] $، وهو فاصل مغلق.

هاتان المجموعتان مغلقتان في الطوبولوجيا القياسية، ولا توجد بينهما أي نقطة مشتركة، وبالتالي فهما منفصلتان.

مثال

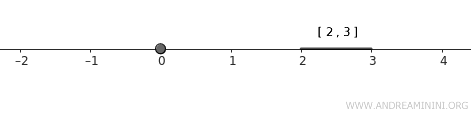
ملاحظة. تتكون $ A $ من نقطة واحدة فقط، مما يجعلها مغلقة في الطوبولوجيا القياسية. أما $ B $ فهو فاصل مغلق، ولذلك فهو أيضاً مجموعة مغلقة.

نبحث الآن عن مجموعتين مفتوحتين منفصلتين تحتويان المجموعتين $ A $ و $ B $.

يمكن اختيار $ U = (-1, 1) $ جواراً مفتوحاً يحتوي المجموعة $ A = \{0\} $.

$$ A \subset U = (-1,1) $$

كما يمكن اختيار $ V = (1, 4) $ جواراً مفتوحاً يحتوي المجموعة $ B = [2,3] $ بالكامل.

$$ B \subset V = (1,4) $$

من الواضح أن $ U $ و $ V $ منفصلان لأن $ U \cap V = \emptyset $. وهذا يبرهن أن $ \mathbb{R} $ بالطوبولوجيا القياسية فضاء طبيعي.

مثال

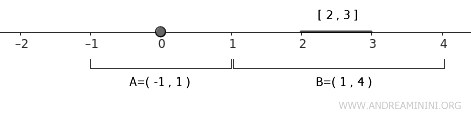
وينطبق هذا المبدأ على أي زوج من المجموعات المغلقة المنفصلة، إذ يمكن دائماً إيجاد جوارين مفتوحين منفصلين يحتويانها.

وبذلك فإن خط الأعداد $ X = \mathbb{R} $ المزود بالطوبولوجيا القياسية يُعد مثالاً نموذجياً للفضاء الطبيعي.

ملاحظات إضافية

إليك بعض النقاط الأساسية المتعلقة بالفضاءات الطبيعية:

خط الأعداد $ \mathbb{R} $ فضاء طبيعي
فهو لا يحقق فقط خاصية الانتظام التي تتيح فصل نقطة عن مجموعة مغلقة بواسطة جوارين مفتوحين منفصلين، بل يحقق أيضاً خاصية الطبيعية التي تُعد أقوى.
كل فضاء متري فضاء طبيعي
فوجود مقياس يحدد المسافات بين النقاط يضمن تحقق قدرة الفضاء على فصل المجموعات المغلقة المنفصلة.
كل فضاء طبيعي فضاء منتظم
مما يعني أن خاصية الطبيعية أقوى من خاصية الانتظام.

وهكذا تتضح أهمية خاصية الطبيعية في فهم البنية التبولوجية للفضاءات وتحليلها.