المجموعات المفتوحة

نقول إن المجموعة A هي مجموعة مفتوحة إذا تحقق أنه، لكل عنصر x ينتمي إلى المجموعة (x∈A)، يوجد جوار لنقطة x يكون بأكمله محتوى داخل المجموعة نفسها.

 

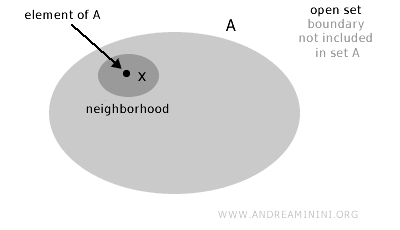
وبصياغة حدسية، تكون المجموعة مفتوحة عندما لا تنتمي نقاط حدودها إلى عناصرها الداخلية.

أما في الصياغة الرياضية الدقيقة، فالمجموعة A ضمن الفضاء الطوبولوجي X تكون مفتوحة إذا تحقق أنه، لكل نقطة x في A، يوجد جوار كامل لـ x يقع بكامله داخل المجموعة A.

ملاحظة. يعني ذلك أن كل نقطة داخل المجموعة يمكن إحاطتها بمنطقة صغيرة تقع بأكملها داخل المجموعة دون ملامسة الحدود الخارجية.

مثال تطبيقي

من أبسط الأمثلة في البعد الواحد الفترة المفتوحة على خط الأعداد الحقيقية.

ما هي الفترة المفتوحة؟ الفترة المفتوحة على \( \mathbb{R} \) هي مجموعة الأعداد الحقيقية \( x \) التي تحقق \( a < x < b \)، حيث a و b عددان حقيقيان مع الشرط \( a < b \).

تُكتب الفترة بالشكل (a,b)، وتشير الأقواس المستديرة إلى أن النقطتين a و b غير داخلتين ضمن عناصر المجموعة.

فعلى سبيل المثال، تُعد الفترة المفتوحة (3,10) مجموعة مفتوحة على خط الأعداد الحقيقي.

في هذه الحالة، تتكون المجموعة A من عدد غير منتهٍ من القيم الواقعة بين 3 و 10 دون شمول الطرفين.

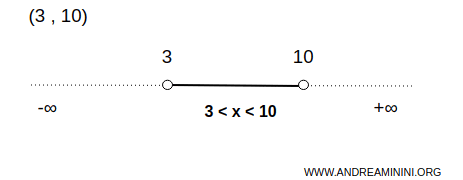
وهذا يعني أنه، لكل نقطة x داخل هذه الفترة، يمكن دائما إيجاد فترة مفتوحة أصغر تقع بكاملها داخل (3,10).

فعلى سبيل المثال، عند النقطة ‎x=3.1‎ يمكن اختيار الفترة المفتوحة ‎(3.09,3.11)‎ وهي بكاملها داخل الفترة (3,10).

وتسري النتيجة نفسها على أي نقطة داخل الفترة، لأن كل عددين حقيقيين يمكن دائماً أن يقع بينهما عدد غير منتهٍ من الأعداد الحقيقية.

ملاحظة. حتى عند اختيار عدد قريب جدا من أحد الطرفين، مثل ‎3.001‎، يمكن دائما تكوين جوار صغير للغاية على صورة ‎3.001±0.00000001‎ يضم عددا غير منتهٍ من القيم داخل الفترة المفتوحة (3,10).

يمثل هذا مثالا بسيطا لمجموعة مفتوحة في بعد واحد.

أمثلة أخرى

يمكن تعميم المفهوم على البعد الثاني، مثل المستوى الإحداثي.

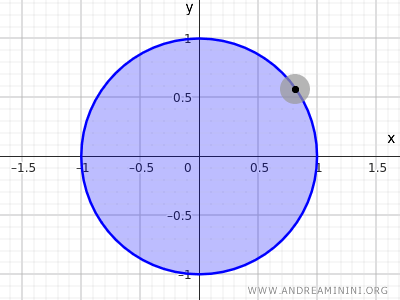
على سبيل المثال، ننظر إلى مجموعة النقاط التي تحقق متباينة دائرة نصف قطرها r=1 ومركزها (0,0).

$$ x^2+y^2<1 $$

تصف هذه المتباينة مجموعة النقاط التي يقل بعدها عن 1 عن المركز (0,0)، أي دون تضمين نقاط المحيط وإنما نقاط داخل الدائرة فقط.

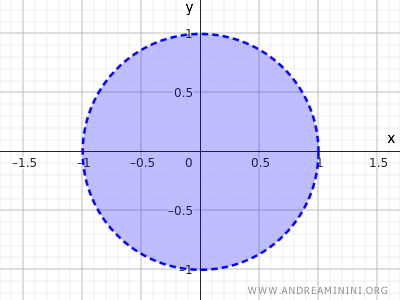
وهذا مثال آخر لمجموعة مفتوحة.

متى تكون المجموعة مغلقة؟

لكي نحصل على مجموعة مغلقة، نضيف نقاط المحيط إلى المجموعة:

$$ x^2+y^2 \le 1 $$

في هذه الحالة لا يعود الشرط الخاص بكل نقطة (امتلاك جوار كامل يقع داخل المجموعة) متحققا عند نقاط المحيط.

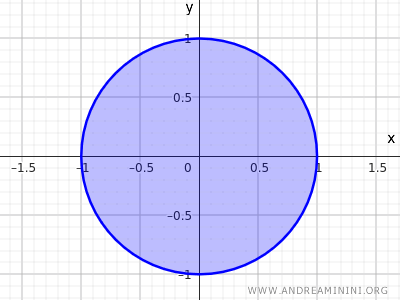
فالنقاط الواقعة على المحيط لا تمتلك أي جوار كامل يقع داخل المجموعة.

ملاحظة. في الطوبولوجيا، لا تُعد معادلة الدائرة ‎\(x^2+y^2=1\)‎ مجموعة مفتوحة ولا مغلقة في الفضاء الإقليدي ‎\( \mathbb{R}^2 \) لأنها تمثل نقاط المحيط فقط دون النقاط الداخلية. أما المتباينة ‎\(x^2+y^2<1\)‎ فهي مثال لمجموعة مفتوحة، بينما تمثل ‎\(x^2+y^2\le 1\)‎ مجموعة مغلقة لأنها تضم النقاط الداخلية ونقاط المحيط معا.

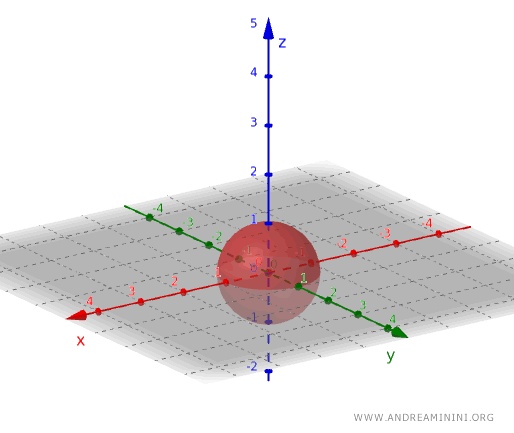
وبالطريقة نفسها يمكن في البعد الثالث تكوين مجموعة مفتوحة بالنظر إلى مجموعة النقاط داخل كرة ما دون تضمين نقاط سطحها.

اختيار الطوبولوجيا

تُعد الفترات المفتوحة مثالا تعليميا مفيدا لأنها توضح الفكرة بشكل بديهي.

غير أن مفهوم المجموعة المفتوحة أوسع بكثير ولا يقتصر على الفترات أو الأقراص المفتوحة.

وبعد استيعاب الفكرة الأساسية، يصبح من الضروري توسيع النظرة إلى المفهوم الطوبولوجي العام.

إن مفهوم "المجموعة المفتوحة" يعتمد على الطوبولوجيا المعتمدة على الفضاء محل الدراسة.

والفكرة الجوهرية هي أن تعريف الانفتاح قد يختلف جذريا من طوبولوجيا إلى أخرى.

فقد تكون مجموعة ما مغلقة في طوبولوجيا مألوفة، بينما تُعد مفتوحة في طوبولوجيا أخرى.

وبمعنى مباشر، يمكن أن تُعد أي مجموعة مفتوحة إذا تغيرت الطوبولوجيا المعتمدة على الفضاء.

ما هي الطوبولوجيا؟ الطوبولوجيا على فضاء ما هي مجموعة من المجموعات التي تُعد مفتوحة وفق قواعد محددة، من بينها أن اجتماع عدد غير منتهٍ من المجموعات المفتوحة يبقى مجموعة مفتوحة، وأن تقاطع عدد منتهٍ منها يبقى مجموعة مفتوحة أيضا.

لذلك لا ينبغي حصر مفهوم الانفتاح في أمثلة مألوفة محدودة، مثل الفترات أو الأقراص المفتوحة.

ففي الطوبولوجيا، قد تشمل المجموعات المفتوحة أنواعا عديدة من المجموعات التي لا تبدو بديهية للوهلة الأولى.

مثال تطبيقي

لننظر إلى الفضاء \( \{a, b\} \) المكوّن من عنصرين فقط.

يمكن تعريف طوبولوجيتين مختلفتين على هذا الفضاء: الطوبولوجيا التافهة والطوبولوجيا المنفصلة.

• الطوبولوجيا التافهة
  في هذه الطوبولوجيا لا تكون المجموعات المفتوحة سوى المجموعة الخالية \( \emptyset \) والمجموعة الكلية \( \{a, b\} \). وهي أبسط طوبولوجيا ممكنة لأنها لا تمنح أي بنية مفتوحة غير هاتين المجموعتين.
• الطوبولوجيا المنفصلة
  في الطوبولوجيا المنفصلة تُعد كل مجموعة جزئية من \( \{a, b\} \) مجموعة مفتوحة. وهذا يعني أن \( \{a\} \) و \( \{b\} \) و \( \{a, b\} \) و \( \emptyset \) كلها مجموعات مفتوحة. وتُعد هذه الطوبولوجيا الأغنى لأنها تعتبر كل تركيب ممكن من العناصر مجموعة مفتوحة.

ننظر الآن إلى المجموعة \( \{a\} \) في هاتين الطوبولوجيتين:

• في الطوبولوجيا التافهة، لا تُعد {a} مجموعة مفتوحة
  فالمجموعة المفتوحة الوحيدة غير الخالية هي \( \{a, b\} \).
• في الطوبولوجيا المنفصلة، تُعد {a} مجموعة مفتوحة
  لأن كل مجموعة جزئية من الفضاء تُعد مفتوحة بحكم التعريف.

وبذلك تكون \( \{a\} \) مجموعة مفتوحة في الطوبولوجيا المنفصلة، لكنها ليست كذلك في الطوبولوجيا التافهة.

يوضح هذا المثال بصورة جلية أن مفهوم الانفتاح مرتبط ارتباطا مباشرا بالطوبولوجيا المختارة.

مبرهنة في المجموعات المفتوحة

المبرهنة 1

لتكن \( X \) مجموعة و \( T \) طوبولوجيا عليها بحيث يشكّلان الفضاء الطوبولوجي \( (X, T) \). عندئذ تكون المجموعة الجزئية \( S \subset X \) مجموعة مفتوحة في الفضاء \( (X, T) \) إذا تحقق أنه، لكل عنصر \( s \in S \)، يوجد جوار مفتوح \( U \) لهذا العنصر بحيث يكون \( U \subset S \).

وبحسب التعريف، تُعد المجموعة \( S \) مفتوحة لأنها تنتمي إلى البنية الطوبولوجية المحددة على \( X \).

وبذلك يمكن النظر إلى المجموعة \( S \) بوصفها تضم حول كل عنصر فيها جوارا كاملا يقع داخلها.

ومن هنا نستنتج أن الجوار \( U_s \) لكل عنصر \( s \in S \) هو مجموعة مفتوحة محتواة في \( S \).

$$ x \in U_s \subset S \subset X $$

وبصورة عامة، يمكن تمثيل المجموعة المفتوحة على أنها اتحاد لجيران مفتوحين لجميع نقاطها.

وبالتالي، إذا تحقق أن لكل عنصر \( s \) في المجموعة \( S \) جوارا مفتوحا \( U_s \subset S \)، أمكن القول إن \( S \) مجموعة مفتوحة لأنها اتحاد مجموعات مفتوحة.

وبصيغة مكافئة، تكون المجموعة مفتوحة إذا وفقط إذا وُجد لكل نقطة داخلها جوار مفتوح يقع بأكمله ضمن هذه المجموعة.

مثال. تخيّل منضدة تنتشر عليها كرات زجاجية. كل كرة تمثل نقطة في مجموعة ما. القول إن هذه المجموعة "مفتوحة" يعني وجود حيّز حول كل كرة يسمح لها بالحركة داخل سطح المنضدة دون أن تلامس الحافة. فإذا أمكن رسم دائرة حول كل كرة بحيث تقع الدائرة بأكملها فوق سطح المنضدة دون تجاوز الأطراف، فإن مجموعة هذه الكرات تمثل "مجموعة مفتوحة". فجوهر الفكرة أن لكل كرة مساحة داخل المجموعة تتيح لها الحركة دون بلوغ الحدود.

المبرهنة 2

لتكن \( X \) مجموعة و \( B \) أساسا لطوبولوجيا على \( X \). تكون المجموعة \( A \subset X \) مجموعة مفتوحة في الطوبولوجيا المولَّدة بالأساس \( B \) إذا وفقط إذا تحقق أنه، لكل عنصر \( x \in A \)، يوجد عنصر أساس \( B_x \in B \) بحيث \( x \in B_x \) و \( B_x \subseteq A \).

تبرز هذه المبرهنة خاصية أساسية للطوبولوجيا المتولدة عن أساس.

فلا بُدّ لكل عنصر داخل \( A \) من وجود "جوار قاعدي" ينتمي إلى عناصر الأساس، ويقع بأكمله داخل \( A \).

وهذا يكفي لإثبات أن \( A \) مجموعة مفتوحة في الطوبولوجيا المتولدة عن \( B \).

البرهان. بما أن \( A \) مجموعة مفتوحة في الطوبولوجيا المتولدة عن الأساس \( B \)، فهذا يعني - وفق التعريف - أن \( A \) اتحاد عناصر الأساس. ومن ثم فإن كل عنصر \( x \in A \) ينتمي إلى مجموعة أساس واحدة على الأقل \( B_x \)، وتكون \( B_x \subseteq A \). والعكس صحيح كذلك: فإذا تحقق لكل عنصر \( x \in A \) وجود عنصر أساس \( B_x \subseteq A \)، فإن \( A \) اتحاد لمجموعات أساس، أي إن \( A \) مجموعة مفتوحة في الطوبولوجيا المولدة عن \( B \).

مثال

لنأخذ \( X = \{1, 2, 3, 4, 5\} \) والأساس \( B = \{\{1\}, \{2, 3\}, \{4, 5\}\} \). نريد التحقق مما إذا كانت المجموعة \( A = \{1, 2, 3\} \) مفتوحة.

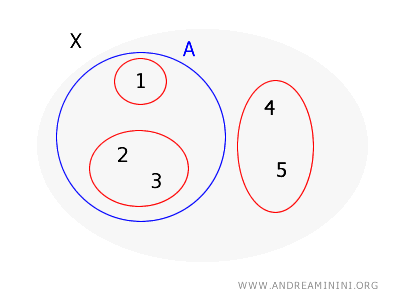
لكل عنصر في \( A \) نبحث عن مجموعة أساس تحتويه وتقع بأكملها ضمن \( A \):

• بالنسبة للعنصر \( 1 \)، نجد مجموعة الأساس \( \{1\} \) وتتحقق فيها الشروط.
• بالنسبة للعنصر \( 2 \)، نجد مجموعة الأساس \( \{2, 3\} \) وتتحقق فيها الشروط.
• بالنسبة للعنصر \( 3 \)، نجد المجموعة نفسها \( \{2, 3\} \) وتتحقق فيها الشروط.

بذلك يتبين أن كل عنصر في \( A \) يمتلك جوارا قاعديا محتوى تماما داخل \( A \)، فيتحقق الشرط المطلوب.

وعليه نستنتج أن \( A \) مجموعة مفتوحة في الطوبولوجيا المتولدة عن الأساس \( B \).

مثال 2

نستخدم المجموعة نفسها \( X = \{1, 2, 3, 4, 5\} \) والأساس نفسه \( B = \{\{1\}, \{2, 3\}, \{4, 5\}\} \).

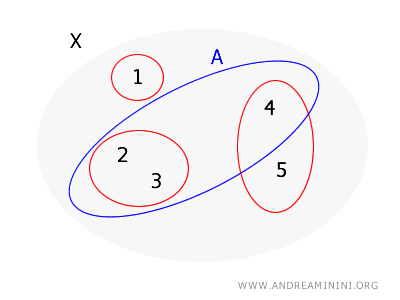
هذه المرة نريد التحقق مما إذا كانت \( A = \{2, 3, 4\} \) مجموعة مفتوحة.

• بالنسبة للعنصر \( 2 \)، نجد مجموعة الأساس \( \{2, 3\} \) وتتحقق فيها الشروط.
• بالنسبة للعنصر \( 3 \)، نجد المجموعة نفسها وتتحقق فيها الشروط.
• بالنسبة للعنصر \( 4 \)، لا نجد أي مجموعة أساس محتواة بالكامل داخل \( A \)، لأن المجموعة الوحيدة التي تحتوي 4 هي \( \{4, 5\} \) وهي لا تقع بكاملها داخل \( A \).

وعليه، ووفقا للمبرهنة، ليست \( A \) مجموعة مفتوحة في الطوبولوجيا المتولدة عن الأساس \( B \)، لأنها لا تحقق شرط الجوار لكل عنصر فيها.

ملاحظات إضافية

بعض النقاط المكملة المتعلقة بالمجموعات المفتوحة:

• تكون المجموعة \( A \) مفتوحة إذا وفقط إذا \( A = \text{Int}(A) \)
  تكون \( A \) في الفضاء الطوبولوجي \( X \) مفتوحة إذا تطابقت مع داخلها. وتُعرَّف داخلية المجموعة - ويرمز لها \( \text{Int}(A) \) - بأنها اتحاد جميع المجموعات المفتوحة المحتواة في \( A \). $$ A = \text{Int}(A) $$

وهكذا دواليك.