أساس الطوبولوجيا

يشير أساس الطوبولوجيا إلى مجموعة B من المجموعات المفتوحة التي يمكن من خلالها توليد كل مجموعة مفتوحة في الفضاء الطوبولوجي T على هيئة اتحاد لمجموعات تنتمي إلى الأساس B.

عندما تكون لدينا مجموعة X وطوبولوجيا T معرفة على X، فإن أساس الطوبولوجيا هو مجموعة B من المجموعات تُسمّى العناصر الأساسية، وتستوفي الشروط الآتية:

• كل عنصر x في المجموعة X يجب أن ينتمي إلى مجموعة واحدة على الأقل من مجموعات B.
• إذا كان عنصر x ينتمي إلى التقاطع غير الفارغ B₁∩B₂ لمجموعتين من B، فيجب أن توجد مجموعة B₃ ضمن التقاطع تحتوي على x، أي أن العنصر x يمكن تغطيته بعنصر أساسي داخل هذا التقاطع.
  

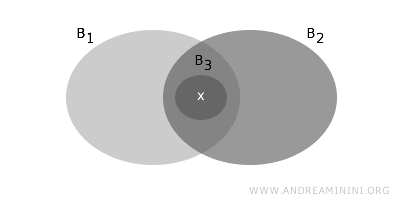
تضمن هذه الشروط أن المجموعة B تشكّل أساساً صالحاً للطوبولوجيا T.

أهمية الأساس

يسمح أساس الطوبولوجيا ببناء الطوبولوجيا T من خلال اتحاد العناصر الأساسية، مما يُغني عن تعداد جميع المجموعات المفتوحة المكوّنة لها.

ملاحظة. الشرط المتعلق بتقاطعات العناصر الأساسية يضمن تحقق المسلّمات الجوهرية للطوبولوجيا، ومنها أن تقاطع مجموعتين مفتوحتين يبقى مجموعة مفتوحة.

مثال تطبيقي

لننظر في المجموعة X

$$ \{a, b, c \} $$

والطوبولوجيا T

$$ T = \{ \emptyset, \{ a \}, \{ b,c \}, \{ a,b,c \} \} $$

تمثل T جميع المجموعات المفتوحة على X.

يمكن اختيار الأساس B كما يأتي:

$$ B = \{ \{ a \} ,\{ b,c \} \} $$

هذا الأساس صحيح لأنه يغطي عناصر X كلها، كما أن مجموعاته لا تنتج تقاطعات تحتاج إلى معالجة إضافية.

ويمكن كتابة كل مجموعة مفتوحة في T على هيئة اتحاد لمجموعات من B:

$$ \{ a \} \in B $$

$$ \{ b,c \} \in B $$

$$ \{ a,b,c \} = \{ a \} \cup \{ b,c \} $$

ملاحظة. في نظرية المجموعات، تُعد المجموعة الخالية Ø  مجموعة جزئية غير حقيقية لأي مجموعة، وهي مدرجة دائماً بالتعريف. $$ \emptyset \in B $$ كما أن المجموعة الخالية مجموعة مفتوحة في أي طوبولوجيا.

يوضح هذا المثال كيفية توصيف المجموعات المفتوحة في حالة الفضاءات المحدودة.

وفي الفضاءات غير المتناهية أو الأكثر تعقيداً، قد تصبح دراسة الأساس وتطبيقاته أكثر دقة، غير أن المبدأ ذاته يظل قائماً: الأساس هو الهيكل الذي تُبنى منه جميع المجموعات المفتوحة.

مقاربة بديلة

من الأساسات الممكنة للطوبولوجيا على X={a,b,c} أيضاً:

$$ B = \{ \{ a \} ,\{ b \}, \{ c \} \} $$

وفي هذا الأساس تغطَّى المجموعة X كلها بمجموعاتها الأحادية. ويمكن التحقق من أنه أساس للطوبولوجيا T={ Ø,X,{a},{b,c}} وفقاً لما يأتي:

• المجموعة الخالية Ø مجموعة مفتوحة بالتعريف، كما أنها مجموعة جزئية غير حقيقية لأي مجموعة.
• {a} مجموعة أساسية ظاهرة. $$ \{ a \} \in B $$
• يمكن الحصول على {b,c} من اتحاد {b} و{c}. $$ \{ b,c \} = \{ b \} \cup \{ c \} $$
• ويُبنى الفضاء كله X من اتحاد {a} و{b} و{c}. $$ \{ a,b,c \} = \{ a \} \cup \{ b \} \cup \{ c \} $$

وبذلك يعمل B كأساس للطوبولوجيا لأنه يتيح توليد جميع المجموعات المفتوحة في T.

ملاحظة. يبيّن هذا المثال أن للطوبولوجيا الواحدة أكثر من أساس، وأن كل أساس يمثل طريقة مختلفة لتوليد مجموعاتها المفتوحة.

مثال 2

لتكن B مجموعة جميع الفترات الحقيقية المفتوحة (a,b) حيث a< b، وهي تغطي خط الأعداد كله:

$$ B=\{ \ (a,b) ⊂ \ R \ | \ a < b \ \} $$

تشكّل هذه المجموعة أساساً للطوبولوجيا الاعتيادية على R، لأن كل نقطة في R تقع ضمن فترة مفتوحة.

وإذا تقاطعت فترتان مفتوحتان، فإن أي نقطة في التقاطع يمكن إيجاد فترة مفتوحة أصغر ضمن التقاطع تحتوي تلك النقطة، وتنتمي إلى B.

فعلى سبيل المثال، عند تقاطع الفترتين (0, 3) و(2, 4)، يكون التقاطع الفترة المفتوحة (2,3).

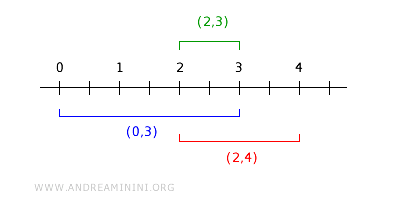
تمثل الفترة (2,3) عنصراً أساسياً B_i ضمن الأساس B وتقع داخل التقاطع. $$ (0,3) \cap (2,4) = (2,3) ∈  B_i ⊂ (0,3) \cap (2,4) ⊂ B $$

أساس قابل للعدّ

الأساس القابل للعدّ في طوبولوجيا على فضاء \( X \) هو مجموعة قابلة للعدّ من المجموعات المفتوحة \( \mathcal{B} = \{B_1, B_2, B_3, \dots\} \) بحيث يمكن تمثيل كل مجموعة مفتوحة في \( X \) على أنها اتحاد لمجموعات تنتمي إلى \( \mathcal{B} \).

تُوصَف مجموعة بأنها قابلة للعدّ إذا كانت منتهية، أو إذا أمكن إقامة تقابل واحد لواحد بينها وبين مجموعة الأعداد الطبيعية \( \mathbb{N} \).

وبعبارة أخرى، تكون المجموعة قابلة للعدّ إذا أمكن فهرستها على الشكل \( B_1, B_2, B_3, \dots \).

ما الفرق بين الأساس والأساس القابل للعدّ؟

كل أساس يولّد الطوبولوجيا، غير أن الأسس التي تتكوّن من عدد قابل للعدّ من المجموعات فقط هي التي تُسمّى أسساً قابلة للعدّ.

أهمية الأساس القابل للعدّ. امتلاك أساس قابل للعدّ خاصية مهمّة في الطوبولوجيا. فهو أحد الشروط الرئيسة في مبرهنة أوريسون للتمتير، كما أن كثيراً من نتائج التحليل والطوبولوجيا تنطبق فقط أو تصبح أكثر بساطة في الفضاءات ذات الأساس القابل للعدّ.

مثال

في \( \mathbb{R} \) المزود بالطوبولوجيا القياسية، تُعد مجموعة الفترات المفتوحة \( (a, b) \) ذات النهايتين العقلانيتين \( a, b \in \mathbb{Q} \) مع شرط \( a < b \) أساساً قابلاً للعدّ.

فجميع هذه الفترات يمكن ترتيبها في تسلسل يمكن فهرسته.

برهان

مجموعة الأعداد الطبيعية قابلة للعدّ لأنها تُرتَّب كما يأتي:

\[ 1,\ 2,\ 3,\ 4,\ 5,\ \dots \]

وإذا أمكن بناء تسلسل مشابه لجميع الفترات المفتوحة ذات الأطراف العقلانية حيث \( a < b \)، فستكون تلك المجموعة أيضاً قابلة للعدّ.

وعلى الرغم من أن \( \mathbb{Q} \) مجموعة غير منتهية، فإنها قابلة للعدّ. فمثلاً، يمكن ترتيبها على النحو:

\[ 0,\ 1,\ -1,\ \tfrac{1}{2},\ -\tfrac{1}{2},\ \tfrac{2}{3},\ -\tfrac{2}{3},\ \dots \]

ولنرمز إلى عناصرها بالترتيب: \( q_1, q_2, q_3, \dots \).

وعندئذ يمكن اعتبار جميع الأزواج \( (q_i, q_j) \) التي تحقق \( q_i < q_j \). كل زوج من هذا النوع يحدد فترة مفتوحة.

• \( (q_1, q_2) = (0, 1) \)
• \( (q_3, q_2) = (-1, 1) \)
• \( (q_4, q_5) = (\tfrac{1}{2}, -\tfrac{1}{2}) \) ❌ مُستبعَد لأن شرط \( a < b \) غير محقق
• \( (q_5, q_1) = (-\tfrac{1}{2}, 0) \)
• ...

كل فترة صحيحة (أي التي تحقق \( a < b \)) يمكن إدراجها ضمن قائمة مرتبة، على نحو:

1. \( (0, 1) \)
2. \( (-1, 1) \)
3. \( (-\tfrac{1}{2}, 0) \)
4. \( (0, \tfrac{1}{2}) \)
5. \( (-1, \tfrac{1}{2}) \)
6. \( (\tfrac{1}{2}, 1) \)
7. \( (-\tfrac{2}{3}, 0) \)
8. \( (0, \tfrac{2}{3}) \)
9. \( (-1, \tfrac{2}{3}) \)
10. \( (-\tfrac{1}{2}, \tfrac{1}{2}) \)
11. ...

الخلاصة: على الرغم من أن عدد هذه الفترات غير منتهٍ، فإنها قابلة للترتيب على نسق يشبه تسلسل الأعداد الطبيعية. وهذا هو جوهر مفهوم «القابليّة للعدّ».

وبالتالي، فإن مجموعة الفترات \( (a, b) \) ذات الأطراف العقلانية حيث \( a < b \) مجموعة قابلة للعدّ لأنها قابلة للإحصاء دون إغفال أي عنصر.

ملاحظات

فيما يلي بعض الملاحظات الإضافية حول أسس الطوبولوجيا:

• إذا أخذنا مجموعة X وأنشأنا أساساً B بحيث تكون كل مجموعة من الشكل {x} عنصراً في B لكل x∈X، أمكن توليد أي طوبولوجيا T على X.

  فالمجموعات الأحادية تكوّن أساساً عاماً يمكن منه الحصول على جميع الطوبولوجيات الممكنة على X عن طريق اتحاداتها.
  
  فمثلاً، الأساس B = { {a}, {b}, {c} } يولّد الطوبولوجيا T={Ø,{a},{b,c},X}.
  
  كما يمكن للأساس نفسه توليد طوبولوجيات أخرى، مثل T={Ø,{b},{a,c},X}، أو الطوبولوجيا التافهة T={Ø, X}، أو الطوبولوجيا المنفصلة T={Ø,{a},{b},{c},{a,b},{a,c},{b,c},X}، وغيرها.

  ملاحظة. الشرط الأول محقق لأن كل عنصر من عناصر X يظهر في مجموعة من B. والشرط الثاني محقق لأن المجموعات الأحادية متمايزة بطبيعتها لكون كل منها يضم عنصراً واحداً فقط.

وما إلى ذلك.