طوبولوجيا الصناديق المفتوحة

تقوم طوبولوجيا الصناديق المفتوحة على فكرة بسيطة ومباشرة. ففي المستوى \( \mathbb{R}^2 \)، نعتبر أي اتحاد من صناديق مفتوحة مجموعة مفتوحة. والصندوق المفتوح ليس إلا حاصل ضرب لفترتين مفتوحتين على محوري الإحداثيات، مما يمنحنا طريقة واضحة لرسم الأجواء المحيطة بالنقاط في بعدين.

تعتمد هذه الطوبولوجيا على قاعدة تتكون كليا من صناديق مفتوحة. وهذه الصناديق تعمل كعناصر أساسية نبني منها مجموعات مفتوحة أكبر وأكثر تعقيدا.

وبعبارة أوضح، يكون الجزء \( U \subseteq \mathbb{R}^2 \) مفتوحا إذا تمكنّا حول كل نقطة \( (x, y) \) داخله من إيجاد صندوق مفتوح يحتويها بالكامل ويقع ضمن \( U \).

بهذه الطريقة تصبح الصناديق المفتوحة جزءا محوريا في فهم طوبولوجيا المستوى الإقليدي.

$$ B = \{ (a, b) \times (c, d) \mid a< b,\, c

وتمثل \( a \) و\( b \) و\( c \) و\( d \) حدود الصندوق المفتوح، بشرط أن تكون كل فترة مفتوحة فعلا، أي أن \( a< b \) و\( c

تقدّم هذه القاعدة طريقة بديلة لوصف طوبولوجيا المستوى مقارنة بالأسلوب المعروف الذي يعتمد على الأجواء الدائرية. كلا الأسلوبين متكافئ من حيث النتائج، لكن الفكرة الهندسية تختلف.

ملاحظة: ما يميز الطوبولوجيا هو مرونتها. فسواء استخدمنا دوائر أو صناديق، فإن الهدف واحد، وهو بناء مجموعات مفتوحة بطريقة تسمح بدراسة البنية العامة للمكان. الشكل الهندسي ليس شرطا، بل الأثر الطوبولوجي هو المهم.

مثال توضيحي

يمكن تخيل الصندوق المفتوح بوصفه ناتجا عن جمع فترتين مفتوحتين، الأولى على محور \( x \) والثانية على محور \( y \).

لنأخذ الفترتين \( (1, 3) \) على محور \( x \) و\( (2, 4) \) على محور \( y \). هاتان الفترتان تحددان منطقة مستطيلة مفتوحة داخل المستوى.

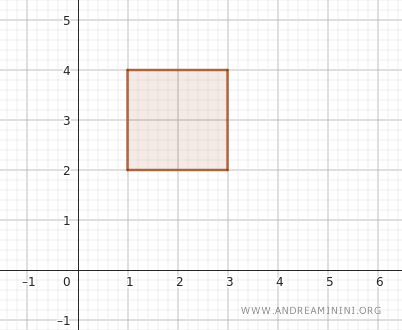
هذه المنطقة تضم كل نقطة \( (x, y) \) يتحقق فيها الشرطان \( 1 < x < 3 \) و\( 2 < y < 4 \). ولهذا يُكتب الصندوق على الشكل \( (1, 3) \times (2, 4) \).

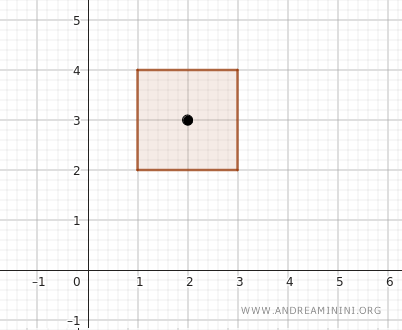
وعند اختيار نقطة مثل \( (2, 3) \) نلاحظ بسهولة أنها تقع بين حدود الفترتين، وبالتالي تنتمي إلى داخل الصندوق.

ملاحظة: من المهم الانتباه إلى أن حدود الصندوق ليست جزءا من المجموعة المفتوحة. أي نقطة تقع على خطوط الحدود تبقى خارج الصندوق، مثل النقاط على \( x = 1 \) أو \( x = 3 \) أو \( y = 2 \) أو \( y = 4 \).