التقابلات في علم الطوبولوجيا
التقابل (Homeomorphism) هو في علم الطوبولوجيا تحويل يعتمد على دالة تقابلية (واحد لواحد وعلى) تكون متصلة، وتكون دالتها العكسية أيضًا متصلة.
بعبارة أخرى، يتيح هذا المفهوم تحويل فضاء طوبولوجي إلى آخر، ثم العودة إلى الفضاء الأصلي من دون أي "تمزيق" أو "لصق".
وبصيغة أبسط، يتيح التقابل تشويه أحد الفضاءات وتحويله إلى آخر بسلاسة تامة، من غير تمزيق أو دمج أي جزء.
على سبيل المثال، يُعد فنجان القهوة المزود بمقبض والدونات (الطارة) متقابلين طوبولوجيًا، لأن كلاً منهما يمكن أن يتحول تدريجيًا إلى الآخر من دون انقطاع في الشكل.

من المنظور الطوبولوجي، يُعتبر الشكلان متكافئين لأن كلاً منهما يحتوي على ثقب واحد، أي الفتحة المركزية في الدونات والفجوة في مقبض الفنجان. يمكننا إعادة تشكيل الفنجان حول مقبضه ليأخذ شكل الدونات.
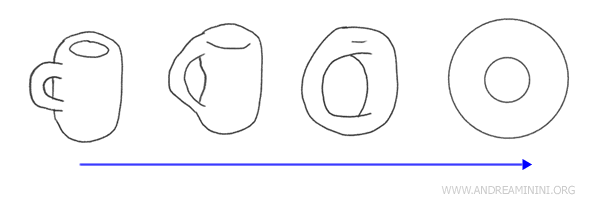
إذا ارتبط فضاءان طوبولوجيان بتقابل، فإنهما يُسميان فضاءين متقابلين، أي أنهما متكافئان طوبولوجيًا حتى وإن اختلفت أشكالهما الهندسية.
خصائص التقابل الطوبولوجي
فيما يلي أهم الخصائص المميزة للتقابل:
- الدالة التقابلية (الواحد لواحد وعلى)
تُنشئ علاقة مطابقة بين عناصر فضاءين، بحيث يقابل كل عنصر في الفضاء الأول عنصر واحد فقط في الفضاء الثاني والعكس صحيح. - الاستمرارية
يكون التقابل دالة مستمرة بطبيعته، أي أن التغييرات الصغيرة في القيم المدخلة تُحدث تغييرات صغيرة في القيم الناتجة. - استمرارية الدالة العكسية
يجب أن تكون الدالة العكسية أيضًا مستمرة، مما يسمح بإجراء التحويل في الاتجاهين من دون فقدان خاصية الاستمرارية. - حفظ الخصائص الطوبولوجية
يحافظ التقابل على الخصائص الجوهرية للطوبولوجيا مثل الاستمرارية والاتصال والانضغاط، مما يعني أن العلاقات البنيوية في الفضاء الأصلي تبقى محفوظة في الفضاء الناتج.
بمعنى أدق، التقابل هو دالة مستمرة قابلة للعكس بين فضاءين طوبولوجيين \(X\) و\(Y\)، بحيث تكون الدالة العكسية أيضًا مستمرة. وبهذا تُحفظ الخصائص الطوبولوجية في كلا الفضاءين.
ببساطة، التقابل هو طريقة لإعادة تشكيل فضاء إلى آخر من دون تمزيق أو دمج، أي أنه يمثل نوعًا من "التطابق المثالي" بين شكلين أو فضاءين.
من المهم تذكّر تعريف الاستمرارية في الطوبولوجيا:
إذا كان لدينا فضاءان طوبولوجيان \(X\) و\(Y\)، فإن الدالة \(f: X \to Y\) تكون مستمرة إذا كانت الصورة العكسية لأي مجموعة مفتوحة \(V\) في \(Y\) مجموعة مفتوحة في \(X\).
بعبارة أخرى، الدالة المستمرة في الطوبولوجيا "تحافظ" على بنية المجموعات المفتوحة عند نقل النقاط من فضاء إلى آخر.
لذلك، تُعد الاستمرارية في الطوبولوجيا صيغة أكثر عمومية وتجريدًا لمفهوم الاستمرارية المعروف في التحليل الرياضي.
ملاحظة: في التحليل الرياضي، تُعرّف الاستمرارية بالاعتماد على المسافة بين النقاط. أما في الطوبولوجيا فتعتمد على بنية المجموعات المفتوحة، وهو مفهوم أوسع لا يتطلب وجود مسافة.
مثال توضيحي
لنفهم فكرة التقابل والاستمرارية بشكل عملي باستخدام مفهوم المجموعات المفتوحة.
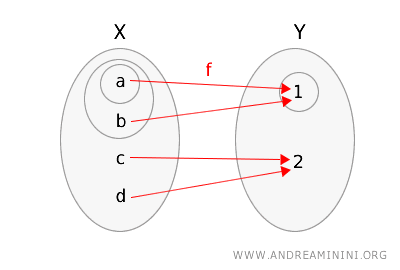
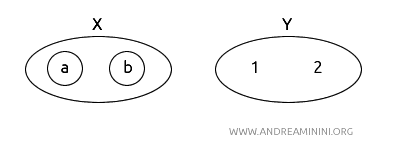
لنعتبر فضاءين طوبولوجيين \(X = \{a, b, c, d\}\) و\(Y = \{1, 2\}\).
- في الفضاء \(X\): المجموعات المفتوحة هي \(\{\}, \{a\}, \{a, b\}, \{a, b, c, d\}\).
- في الفضاء \(Y\): المجموعات المفتوحة هي \(\{\}, \{1\}, \{1, 2\}\).
تكون الدالة \(f: X \rightarrow Y\) مستمرة إذا كانت الصورة العكسية لكل مجموعة مفتوحة في \(Y\) مجموعة مفتوحة في \(X\).
نُعرّف الدالة \(f: X \rightarrow Y\) كما يلي:
\(f(a) = 1\)، \(f(b) = 1\)، \(f(c) = 2\)، \(f(d) = 2\).
ولتوضيح الفكرة، سنُمثّل الدالة \(f\) والفضاءين بتظليل المجموعات المفتوحة.
فلنختبر الآن مدى مطابقة هذه الدالة لتعريف الاستمرارية الطوبولوجية:
- إذا أخذنا المجموعة المفتوحة \(\{1\}\) في \(Y\)، فإن صورتها العكسية هي \(f^{-1}(\{1\}) = \{a, b\}\)، وهي مجموعة مفتوحة في \(X\).
- وإذا أخذنا المجموعة المفتوحة \(\{1, 2\}\) في \(Y\)، فصورتها العكسية هي \(f^{-1}(\{1, 2\}) = \{a, b, c, d\}\)، وهي أيضًا مجموعة مفتوحة في \(X\).
وبما أن الصورة العكسية لكل مجموعة مفتوحة في \(Y\) مجموعة مفتوحة في \(X\)، فإن الدالة \(f\) مستمرة.
ملاحظة: تم استبعاد المجموعة الفارغة لأنها مفتوحة في أي فضاء طوبولوجي بحسب التعريف.
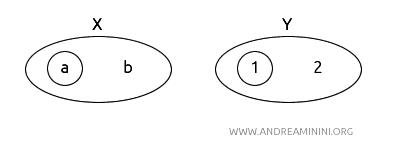
لننظر الآن في دالة مختلفة \(g: X \rightarrow Y\) معرّفة كما يلي:
\(g(a) = 1\)، \(g(b) = 1\)، \(g(c) = 1\)، \(g(d) = 2\).
نُمثّل أيضًا هذه الدالة \(g\) بنفس الطريقة لتوضيح المجموعات المفتوحة في كلا الفضاءين.
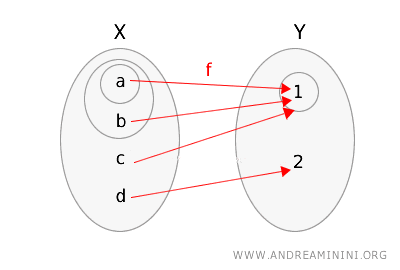
لنفحص ما إذا كانت هذه الدالة تحقق شرط الاستمرارية.
- إذا أخذنا المجموعة المفتوحة \(\{1\}\) في \(Y\)، فإن صورتها العكسية في \(X\) هي \(g^{-1}(\{1\}) = \{a, b, c\}\)، وهي ليست مجموعة مفتوحة في \(X\).
إذًا، بما أن هناك مجموعة مفتوحة واحدة على الأقل في \(Y\) (وهي \(\{1\}\)) صورتها العكسية ليست مفتوحة في \(X\)، فإن الدالة \(g\) غير مستمرة.
ملاحظة: نستنتج أن الدالة تكون مستمرة إذا كانت الصورة العكسية لكل مجموعة مفتوحة في الفضاء الهدف (\(Y\)) مجموعة مفتوحة في الفضاء الأصلي (\(X\)). أما إذا لم يتحقق ذلك، فهي غير مستمرة. في المثال الأول كانت \(f\) مستمرة لأن هذا الشرط تحقق لكل مجموعة مفتوحة في \(Y\). بينما في المثال الثاني، الدالة \(g\) لم تحقق هذا الشرط.
تعريف التقابل
إذا كان لدينا فضاءان طوبولوجيان \( X \) و\( Y \)، ودالة تقابلية \( f: X \to Y \) ذات دالة عكسية \( f^{-1}: Y \to X \)، وكانتا كلتاهما مستمرتين، فإن \( f \) تُسمّى تقابلاً (Homeomorphism)، ويُقال إن الفضاءين \( X \) و\( Y \) متقابلان \( X \cong Y \).
الفضاءات المتقابلة تُعرف أيضًا بأنها متكافئة طوبولوجيًا.
ما معنى ذلك؟
أن يكون فضاءان متقابلين أو متكافئين طوبولوجيًا يعني أنهما "متماثلان جوهريًا" من منظور طوبولوجي، حتى وإن اختلفت أشكالهما الهندسية.
يُبرز هذا التعريف الخصائص الأساسية للتقابل:
- التقابل (واحد لواحد وعلى): يجب أن تكون الدالة \( f: X \to Y \) دالة تقابلية بحيث يقابل كل عنصر من \( X \) عنصرًا واحدًا فقط في \( Y \)، والعكس بالعكس.
- استمرارية \( f \): يجب أن تكون \( f \) مستمرة، أي أن الصورة العكسية لأي مجموعة مفتوحة في \( Y \) مجموعة مفتوحة في \( X \).
- استمرارية \( f^{-1} \): يجب أن تكون الدالة العكسية \( f^{-1}: Y \to X \) مستمرة أيضًا، أي أن الصورة العكسية لأي مجموعة مفتوحة في \( X \) تحت \( f \) مجموعة مفتوحة في \( Y \).
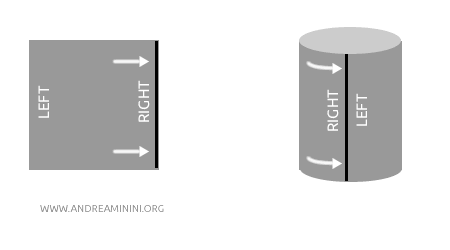
مثال: تخيل أنك تأخذ ورقة مسطّحة وتلفها لتكوّن أسطوانة. تُعد الورقة والأسطوانة متقابلتين طوبولوجيًا لأنك تستطيع تحويل إحداهما إلى الأخرى من دون تمزيق أو لصق، فقط عبر لفّها أو فكّها. تبقى البنية الطوبولوجية (أي المجموعات المفتوحة) كما هي، رغم تغيّر الشكل الهندسي.
من المهم أن نلاحظ أن استمرارية الدالة التقابلية \( f \) لا تقتضي بالضرورة أن تكون دالتها العكسية \( f^{-1} \) مستمرة، إلا إذا كانت \( f \) أيضًا دالة مفتوحة.
أي أن كون \( f \) دالة مستمرة وتقابلية لا يكفي لضمان أن تكون دالتها العكسية \( f^{-1} \) مستمرة، وبالتالي لا يكفي لتكون \( f \) تقابلاً.
في الطوبولوجيا، تُعد الدالة \( f: X \rightarrow Y \) مستمرة إذا كانت الصورة العكسية لكل مجموعة مفتوحة في \( Y \) مجموعة مفتوحة في \( X \).
لكن هذا لا يضمن أن تكون صورة كل مجموعة مفتوحة في \( X \) تحت \( f \) مجموعة مفتوحة في \( Y \).
ولكي تكون الدالة العكسية \( f^{-1} \) مستمرة، يجب أن تكون \( f \) ليست فقط مستمرة وتقابلية، بل أيضًا دالة مفتوحة.
مثال
لننظر في الفضاءين الطوبولوجيين الآتيين:
- \( X = (a, b) \) مزوّد بالطوبولوجيا \( T_X = \{\emptyset, \{a\}, \{b\}, X\} \).
- \( Y = (1, 2) \) مزوّد بالطوبولوجيا \( T_Y = \{\emptyset, Y\} \).
نُعرّف الدالة \( f: X \to Y \) بحيث \( f(a) = 1 \) و\( f(b) = 2 \).
من الواضح أن الدالة \( f \) تقابلية، إذ يقابل كل عنصر في \( X \) عنصرًا واحدًا فقط في \( Y \) والعكس بالعكس.
ملاحظة: في المخطط، تُشير الدوائر إلى المجموعات المفتوحة. فعلى سبيل المثال، المجموعات \(\{a,b\}\)، \(\{a\}\)، و\(\{b\}\) مفتوحة في \( X \)، بينما المجموعة \(\{1,2\}\) مفتوحة في \( Y \). وبحسب التعريف، تُعد المجموعات الفارغة مفتوحة في أي طوبولوجيا، لذلك لم تُعرض في الشكل.
لنحلّل الآن استمرارية \( f \) واستمرارية دالتها العكسية \( f^{-1} \).
- استمرارية الدالة \( f \)
للتحقق من استمرارية \( f \)، ينبغي التأكد من أن الصورة العكسية لكل مجموعة مفتوحة في \( Y \) عبر \( f \) مفتوحة في \( X \). المجموعات المفتوحة في \( Y \) هي \( \emptyset \) و\( Y \):- \( f^{-1}(\emptyset) = \emptyset \)، وهي مفتوحة في \( T_X \).
- \( f^{-1}(Y) = X \)، وهي مفتوحة في \( T_X \).
- استمرارية الدالة العكسية \( f^{-1} \)
نعتبر الآن الدالة العكسية \( f^{-1}: Y \to X \) المعرفة بـ \( f^{-1}(1) = a \) و\( f^{-1}(2) = b \).
للتحقق من استمرارية \( f^{-1} \)، يجب أن تكون الصورة العكسية لكل مجموعة مفتوحة في \( X \) عبر \( f^{-1} \) مفتوحة في \( Y \). المجموعات المفتوحة في \( X \) هي \( \emptyset \)، \(\{a\}\)، \(\{b\}\)، و\( X \):- \( f^{-1}(\emptyset) = \emptyset \)، وهي مفتوحة في \( T_Y \).
- \( f^{-1}(\{a\}) = \{1\} \)، وهي ليست مفتوحة في \( T_Y \) لأن المجموعة الوحيدة المفتوحة في \( T_Y \) التي تحتوي على 1 هي \( Y \).
- \( f^{-1}(\{b\}) = \{2\} \)، وهي ليست مفتوحة في \( T_Y \) للسبب نفسه.
- \( f^{-1}(X) = Y \)، وهي مفتوحة في \( T_Y \).
نستنتج أن \( f \) دالة تقابلية ومستمرّة، ولكن دالتها العكسية \( f^{-1} \) غير مستمرة، وبالتالي فإن \( f \) ليست تقابلاً طوبولوجيًا.
يوضّح هذا المثال أن الدالة التقابلية المستمرة لا تضمن بالضرورة أن تكون دالتها العكسية أيضًا مستمرة.
ملاحظة: في هذا المثال، تعود عدم استمرارية \( f^{-1} \) إلى طبيعة المجموعات المفتوحة في كل من \( X \) و\( Y \): إذ تمتلك \( X \) مجموعات مفتوحة أكثر دقّة (مثل \(\{a\}\) و\(\{b\}\))، بينما تتميّز \( Y \) بطوبولوجيا أبسط لا تحتوي سوى على \( \emptyset \) و\( Y \).
مثال 2
لنأخذ الآن الفضاءين الطوبولوجيين الآتيين:
- \( X = (a, b) \) مزوّد بالطوبولوجيا \( T_X = \{\emptyset, \{a\}, X\} \).
- \( Y = (1, 2) \) مزوّد بالطوبولوجيا \( T_Y = \{\emptyset, \{1\}, Y\} \).
نُعرّف الدالة \( f: X \to Y \) بحيث \( f(a) = 1 \) و\( f(b) = 2 \).
من جديد، الدالة \( f \) تقابلية لأن كل عنصر في \( X \) يقابل عنصرًا وحيدًا في \( Y \) والعكس بالعكس.
دعونا نتحقق من استمرارية \( f \) واستمرارية الدالة العكسية \( f^{-1} \).
- استمرارية الدالة \( f \)
للتحقق من استمرارية \( f \)، ندرس الصورة العكسية لكل مجموعة مفتوحة في \( Y \) عبر \( f \). المجموعات المفتوحة في \( Y \) هي \( \emptyset \)، \(\{1\}\)، و\( Y \):- \( f^{-1}(\emptyset) = \emptyset \)، وهي مفتوحة في \( T_X \).
- \( f^{-1}(Y) = X \)، وهي مفتوحة في \( T_X \).
- \( f^{-1}(\{1\}) = \{a\} \)، وهي مفتوحة في \( T_X \).
- استمرارية الدالة العكسية \( f^{-1} \)
نعتبر الآن الدالة العكسية \( f^{-1}: Y \to X \) المعرفة بـ \( f^{-1}(1) = a \) و\( f^{-1}(2) = b \). للتحقق من استمراريتها، يجب أن تكون الصورة العكسية لكل مجموعة مفتوحة في \( X \) عبر \( f^{-1} \) مفتوحة في \( Y \). المجموعات المفتوحة في \( X \) هي \( \emptyset \)، \(\{a\}\)، و\( X \):- \( f^{-1}(\emptyset) = \emptyset \)، وهي مفتوحة في \( T_Y \).
- \( f^{-1}(\{a\}) = \{1\} \)، وهي مفتوحة في \( T_Y \).
- \( f^{-1}(X) = Y \)، وهي مفتوحة في \( T_Y \).
إذن، في هذه الحالة، الدالة \( f \) تقابلية ومستمرّة، ودالتها العكسية \( f^{-1} \) مستمرّة أيضًا، وبذلك تكون \( f \) تقابلاً طوبولوجيًا.
يكمن الفرق بين هذا المثال وسابقه في اختلاف اختيار الطوبولوجيا على كل من الفضاءين.
ملاحظة: يوضّح هذا المثال أنه باختيار طوبولوجيا مناسبة على \( X \) و\( Y \)، يمكن الحصول على دالة تقابلية مستمرة تمتلك دالة عكسية مستمرة، بخلاف المثال السابق الذي لم يتحقق فيه هذا الشرط.
التمييز بين التقابلات والتحويلات الطوبولوجية الأخرى
على الرغم من أن مصطلح "التقابلات" يُستخدم أحيانًا بشكل عام للإشارة إلى التحويلات الطوبولوجية، فإنه يشير تحديدًا إلى فئة خاصة من هذه التحويلات.
تشترك التحويلات الطوبولوجية والتقابلات في المفهوم الأساسي لكنها تختلف في الصرامة والشروط:
- التحويلات الطوبولوجية
وهي الفئة الأوسع التي تشمل أي تحويل يغيّر الفضاء الطوبولوجي مع الحفاظ على خصائصه البنيوية، مثل الاتصال والاستمرارية. ومن أمثلتها التقابلات، والتحويلات المتجانسة (isotopies)، والهوموتوبيات (homotopies)، والتفاضليات (diffeomorphisms). - التقابلات
وهي التحويلات التي تكون تقابلية ومستمرّة ولها دالة عكسية مستمرة، ما يسمح بتحويل الفضاءات في كلا الاتجاهين دون أي تغيير في بنيتها الطوبولوجية. وتُعد الفضاءات المتقابلة متماثلة طوبولوجيًا حتى وإن اختلفت أشكالها الهندسية.
جميع التقابلات تُعتبر تحويلات طوبولوجية، ولكن ليست كل التحويلات الطوبولوجية تقابلات. فبعضها قد يفتقر إلى خاصية الاستمرارية العكسية أو لا يحقق الشروط المطلوبة للتقابل.
ملاحظات إضافية
فيما يلي بعض التوضيحات المكملة حول مفهوم التقابل:
- الخاصية الطوبولوجية
الخاصية الطوبولوجية هي سمة تبقى محفوظة تحت أي تقابل. أي إذا كان فضاءان متقابلين (أي توجد بينهما دالة تقابلية مستمرة ذات عكس مستمر)، فإنهما يشتركان في جميع الخصائص الطوبولوجية. - مبرهنة هاوسدورف في التقابلات
تنص المبرهنة على أنه إذا كانت \( f: X \to Y \) تقابلاً وكان \( X \) فضاء هاوسدورف، فإن \( Y \) سيكون أيضًا فضاء هاوسدورف. لأن التقابلات تحفظ الخصائص الطوبولوجية، فيرث \( Y \) خاصية هاوسدورف من \( X \). - في الجبر المجرد، المفهوم المناظر للتقابل هو التناظر البنيوي (Isomorphism). ففي التناظر، تحافظ الدالة التقابلية على البنية الجبرية للعمليات، بينما في التقابل الطوبولوجي تُحافظ على بنية المجموعات المفتوحة في الفضاء.
وهكذا تتّضح طبيعة التقابلات في الطوبولوجيا ومعناها العميق.