فضاء هاوسدورف
فضاء هاوسدورف هو أحد المفاهيم الأساسية في الطوبولوجيا، ويتميز بقدرة أي نقطتين متميزتين فيه على امتلاك جوارين مفتوحين ومنفصلين بشكل تام. هذه الخاصية توفر درجة عالية من الفصل الطوبولوجي تجعل التعامل مع هذا النوع من الفضاءات أكثر وضوحاً ومرونة.
الفكرة بسيطة. إذا اخترت أي نقطتين \( x \) و\( y \) في فضاء من نوع هاوسدورف، يمكنك دائماً إيجاد مجموعتين مفتوحتين \( U \) و\( V \) تحيطان بكل نقطة على حدة من دون أي تداخل بينهما. هذا النوع من الانفصال يشبه بشكل ما الحدس الهندسي للمسافة، حتى لو لم يكن الفضاء نفسه مزوداً بمفهوم المسافة.
لهذا السبب، تلعب فضاءات هاوسدورف دوراً مهماً في التحليل الرياضي والهندسة الطوبولوجية، خصوصاً عند دراسة المتتاليات وحدودها.
ومن الخصائص البارزة فيها أن المجموعات أحادية العنصر تعد دائماً مجموعات مغلقة، لأن متممها يكون مفتوحاً.
أمثلة تطبيقية
المثال 1
لنبدأ بالطوبولوجيا القياسية على خط الأعداد الحقيقية \(\mathbb{R}\)، وهي الطوبولوجيا الأكثر شيوعاً في التحليل.

في هذه الطوبولوجيا، النقطة المفردة ليست مجموعة مفتوحة، لأنها لا تضم أي فاصل مفتوح حولها. لكن متمم النقطة المفردة هو دائماً مجموعة مفتوحة.

ولذلك فإن النقطة المفردة نفسها مجموعة مغلقة. هذا يتوافق تماماً مع كون الطوبولوجيا القياسية فضاءً من نوع هاوسدورف، إذ يمكن عزل أي نقطتين متميزتين في فواصل مفتوحة غير متقاطعة.
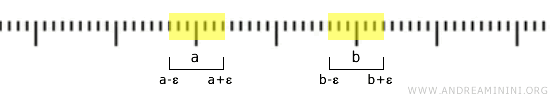
على سبيل المثال، إذا كان \( a < b \)، يمكن اختيار فاصلين مفتوحين صغيرين حول كل منهما بحيث يبقى الفاصلان منفصلين تماماً.
المثال 2
لننظر الآن إلى حالة مختلفة تماماً: الطوبولوجيا المنفصلة على المجموعة X = {1,2,3}. في هذه الطوبولوجيا، كل مجموعة جزئية من X تعد مفتوحة من دون استثناء.
وهذا يعني أن جميع المجموعات الجزئية، بما فيها المجموعات المفردة، مفتوحة. وفي الوقت نفسه، تكون هذه المجموعات أيضاً مغلقة، لأن متمم كل مجموعة مفتوح بدوره.
وبفضل هذا، يصبح الفصل بين أي نقطتين مهمة بسيطة. يمكنك اختيار \( \{x\} \) و\( \{y\} \) كجوارين مفتوحين ومنفصلين لأي عنصرين مختلفين في X.
هل يمكن أن تكون المجموعة مفتوحة ومغلقة في الوقت نفسه؟
في الطوبولوجيا المنفصلة، نعم. كل نقطة مفتوحة لأنها مجموعة جزئية، ومغلقة لأن متممها مجموعة مفتوحة أيضاً. وتسمى هذه المجموعات مجموعات مفتوحة مغلقة.
على سبيل المثال، إذا كانت X={1,2,3} فإن المجموعة {1} مفتوحة، ومتممها {2,3} مفتوح أيضاً، وهذا يجعلها مغلقة في الوقت نفسه.
هذا يوضح الفرق بين الطوبولوجيا المنفصلة والطوبولوجيا القياسية. في الأولى، كل شيء مفتوح ومغلق، بينما في الثانية لا تكون المجموعات المفتوحة إلا تلك التي تحتوي فواصل مفتوحة كاملة حول كل نقطة.
ملاحظات
ميزة مهمة في فضاءات هاوسدورف هي أن المتتاليات لا يمكن أن تمتلك أكثر من حد واحد. فإذا تقاربت المتتالية إلى نقطتين مختلفتين، فلا بد أن تتقاطع جوارات هاتين النقطتين، وهذا يناقض شرط الانفصال.
برهان مختصر: إذا كانت المتتالية xn تقترب من x وy معاً، فلا بد من وجود حد بعده تصبح جميع قيم المتتالية ضمن جوار x وحد آخر تصبح بعده ضمن جوار y. وهذا يعني أن الجوارين يتقاطعان، وهو أمر مستحيل في فضاء هاوسدورف.
هذه الخاصية تجعل فضاءات هاوسدورف بيئة مثالية لدراسة حدود المتتاليات وسلوكها.