الفضاءات المنتظمة في الطوبولوجيا
يُعد الفضاء الطوبولوجي \( X \) منتظماً عندما تتحقق فيه خاصيتان أساسيتان:
- النقطة تشكل مجموعة مغلقة. أي إن كل نقطة في الفضاء تُعامل باعتبارها مجموعة مغلقة ضمن بنيته الطوبولوجية.
- إمكانية فصل نقطة عن مجموعة مغلقة. فإذا كانت لدينا نقطة \( a \in X \) ومجموعة مغلقة \( C \) لا تحتويها، يمكن إيجاد مجموعتين مفتوحتين متباينتين \( U \) و\( V \) بحيث: \[ a \in U, \quad C \subset V, \quad U \cap V = \emptyset \]
تظهر أهمية الفضاءات المنتظمة في قدرتها العالية على الفصل الدقيق بين العناصر. فهي توفر مستوى فصل أقوى من فضاءات هاوسدورف، ما يجعلها مفهوماً مركزياً في دراسة الطوبولوجيا العامة.
وتؤكد مبرهنة أوريشون أن كل فضاء منتظم وله قاعدة قابلة للعد هو فضاء قابل للقياس، مما يمنحه بنية أكثر قابلية للتحليل الرياضي.
مقارنة سريعة مع فضاءات هاوسدورف
في فضاءات هاوسدورف، يكفي أن نستطيع فصل نقطتين متمايزتين بواسطة جوارين مفتوحين. أما في الفضاءات المنتظمة، فيمتد هذا المبدأ ليشمل فصل نقطة عن مجموعة مغلقة بأكملها. وهذا شرط أقوى، ويمنح الفضاء قدرة أعلى على التمييز بين مكوناته.
ملاحظة. الفضاء المنتظم لا يساوي الفضاء الطبيعي. فالأخير يتطلب إمكانية فصل مجموعتين مغلقتين لا تلتقيان بجوارين مفتوحين متباينين. لهذا يكون كل فضاء طبيعي منتظماً، لكن ليست كل الفضاءات المنتظمة فضاءات طبيعية.
ومن المثير للاهتمام أن الانتظام وخصائص الفصل الأخرى لا تتطابق بالضرورة. فقد يكون الفضاء منتظماً دون أن يكون من نوع هاوسدورف، وقد يحدث العكس أيضاً.
مثال تطبيقي يساعد على الفهم
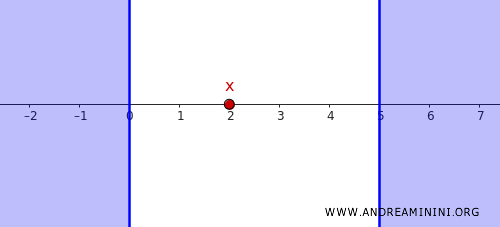
لنأخذ مثالاً مألوفاً. إن خط الأعداد الحقيقية \( \mathbb{R} \) مع الطوبولوجيا القياسية يُعد واحداً من أوضح النماذج على الفضاءات المنتظمة.
افترض لدينا النقطة \( x = 2 \) والمجموعة المغلقة:
\[ C = (-\infty, 0] \cup [5, \infty) \]
من السهل ملاحظة أن \( x \notin C \). والآن نريد إيجاد مجموعات مفتوحة تفصل بينهما.
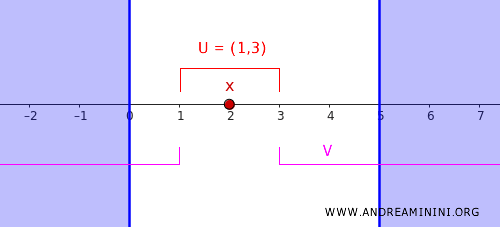
الفترة \( (0,5) \) هي فترة مفتوحة تحتوي \( x \). ومنها يمكن اختيار قيمتين مثل \( c = 1 \) و\( d = 3 \) بحيث تقع النقطة \( 2 \) بينهما:
\[ 0 < c < 2 < d < 5 \]
بهذا تتشكل مجموعتان مفتوحتان:
- \( U = (1,3) \) وتحتوي النقطة \( 2 \).
- \( V = (-\infty, 1) \cup (3, \infty) \) وتحتوي المجموعة \( C \).
هاتان المجموعتان لا تتقاطعان، أي: \[ U \cap V = \emptyset \] وهذا يحقق تماماً تعريف الانتظام.
يمثل هذا المثال طريقة عملية توضح كيف تسمح الطوبولوجيا القياسية بفصل نقطة عن مجموعة مغلقة باستخدام مجموعات مفتوحة متباينة، وهو جوهر مفهوم الفضاء المنتظم.
ملاحظات ختامية
- بديهيات الفصل
تُعد خصائص مثل هاوسدورف والانتظام جزءاً مما يعرف ببديهيات الفصل، وهي أدوات تساعدنا على فهم مدى قدرة الفضاء على التمييز بين نقاطه ومجموعاته.ملاحظة. يمكن النظر إلى خاصية هاوسدورف باعتبارها الحد الأدنى من قدرة الفصل بين النقاط، بينما يقدم الانتظام خطوة إضافية حين يسمح بفصل نقطة عن مجموعة مغلقة لا تشملها. وهذا يعكس دقة أعلى في البنية الطوبولوجية.
يتضح من كل ذلك أن الانتظام خاصية تمنح الفضاء الطوبولوجي قدرة أكبر على الفصل والتحليل، ما يجعلها مفهوماً محورياً لفهم طبيعة البنى الطوبولوجية.