المجموعات المغلقة
يُقال إن مجموعة ما B في فضاء طوبولوجي X هي مجموعة مغلقة إذا كان لكل عنصر ينتمي إلى المتممة u∈X-B جوارٌ يقع بكامله داخل المتممة X-B.
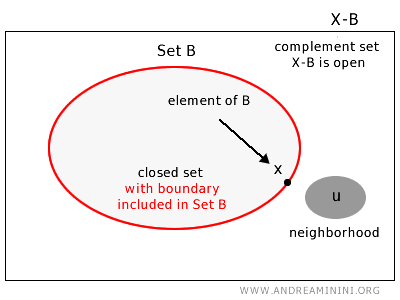
وبعبارة أبسط، تكون المجموعة مغلقة إذا كانت تحتوي جميع نقاط حدودها.
وبصيغة دقيقة، تُعد المجموعة B في الفضاء الطوبولوجي X مغلقة إذا كانت متممتها X-B مجموعة مفتوحة.
ملاحظة: يدل ذلك على وجود عناصر في المجموعة المغلقة B لا يمكن إيجاد جوار لها يكون محتوى بالكامل داخل B.
مثال توضيحي
لننظر إلى خط الأعداد الحقيقية R وأي مجال مغلق.
ما هو المجال المغلق؟ هو مجموعة جميع النقاط x التي تحقق a≤x≤b، حيث a و b عددان حقيقيان بـ $ a \lt b $، وكلاهما داخل المجال.
يُرمز للمجالات المغلقة بالصيغة [a,b]، وتشير الأقواس المربعة إلى شمول النقطتين الطرفيتين a و b.
على سبيل المثال، يُعد المجال [3,10] مجالًا مغلقًا على خط الأعداد الحقيقية.
في هذه الحالة تتكوّن المجموعة B من عدد غير منتهٍ من القيم بين 3 و 10، مع شمول القيمتين الطرفيتين.
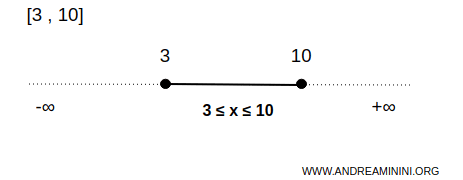
كل نقطة x تحقق 3≤x≤10 تنتمي إلى المجموعة، بما في ذلك 3 و 10 نفسيهما.
مع ذلك، لا تمتلك جميع عناصر المجال جوارًا يقع بالكامل داخل [3,10].
فعلى سبيل المثال، أي جوار للنقطة الحدّية x=3 لا يمكن أن يُحتوى بالكامل داخل المجال المغلق.
ملاحظة: حتى وإن أخذنا جوارًا صغيرًا للغاية مثل 3±0.00000001، فلن يكون بكامله ضمن [3,10] لأن 3-0.00000001 أصغر من 3. وينطبق الأمر نفسه على x=10.
يمثل هذا مثالًا أحادي البعد لمجموعة مغلقة.
أمثلة أخرى على مجموعات مغلقة
يمكن توسيع الفكرة إلى الفضاء ثنائي الأبعاد، أي المستوى.
فمثلًا، مجموعة النقاط التي تحقق معادلة دائرة نصف قطرها r=1 ومركزها عند (0,0):
$$ x^2+y^2≤1 $$
تشمل هذه المجموعة كل النقاط التي يقل أو يساوي بعدها عن المركز 1، أي نقاط المحيط ونقاط الداخل معًا.
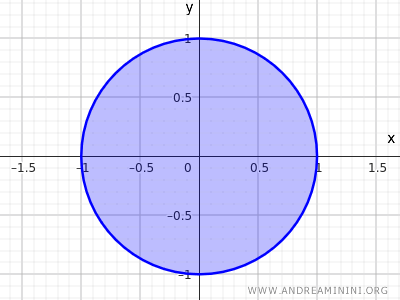
ويُعد ذلك مثالًا آخر على مجموعة مغلقة.
ومن الواضح أن نقاط المحيط لا تمتلك جوارًا يمكن احتواؤه بالكامل داخل المجموعة.
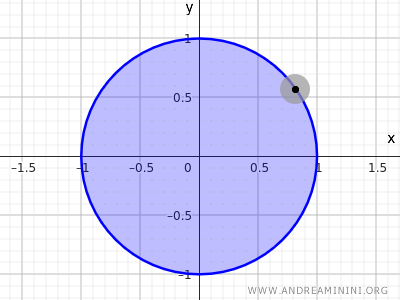
ملاحظة: الدائرة المعرّفة بالمعادلة $ x^2+y^2=1 $ ليست مجموعة مفتوحة ولا مغلقة في الفضاء الإقليدي R2 لأنها تضم نقاط المحيط فقط دون الداخل. أما المجموعة التي تحقق $ x^2+y^2≤1 $ فهي مغلقة لأنها تشمل جميع نقاط الحدود.
وبالأسلوب نفسه، يمتد مفهوم المجموعات المغلقة إلى الفضاء ثلاثي الأبعاد عبر الكرة، ثم إلى الأبعاد الأعلى.
متمّم المجموعة المغلقة
في الفضاء X يكون متمّم المجموعة المغلقة C مجموعة مفتوحة ويُرمز له بـ X-C.
فإذا كانت C مجموعة مغلقة، فإن متممتها X-C مجموعة مفتوحة بالضرورة.
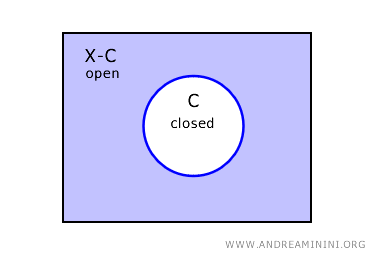
وعكس ذلك صحيح أيضًا: فإذا كانت U مجموعة مفتوحة، فإن متممتها مجموعة مغلقة.
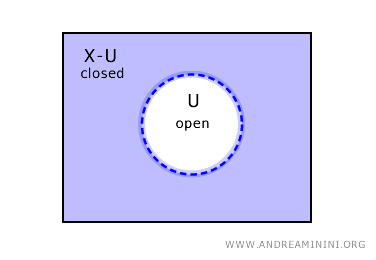
وتجدر الإشارة إلى أن الفضاءات الطوبولوجية قد تحتوي كذلك على مجموعات مفتوحة ومغلقة في آن واحد، بالإضافة إلى مجموعات لا تُعد مفتوحة ولا مغلقة.
وباختصار، لا يعني عدم الإغلاق أن المجموعة مفتوحة، كما أن عدم الانفتاح لا يستلزم الإغلاق.
مثال
لننظر إلى الطوبولوجيا T على المجموعة X={a,b,c,d} التي تضم أربعة عناصر.
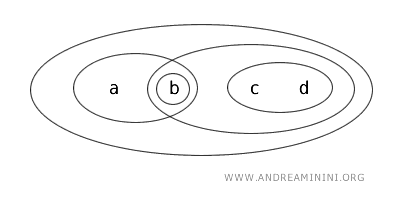
وفقًا للطوبولوجيا T تُعد المجموعات الآتية مجموعات مفتوحة: {b}, {a,b}, {c,d}, {b,c,d}, {a,b,c,d}, ∅.
نستعرض الآن هذه الحالات:
- {b} مجموعة مفتوحة كما تحددها الطوبولوجيا مباشرة.
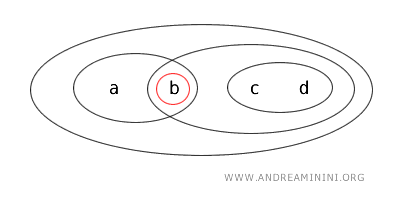
- {a} مجموعة مغلقة لأنها متمّم المجموعة المفتوحة X-{b,c,d}={a}.
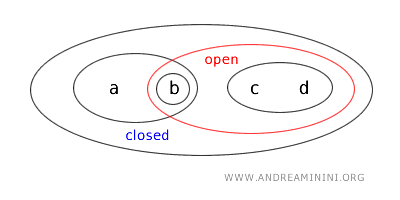
- {a,b} مجموعة مفتوحة ومغلقة في الوقت نفسه. وتُسمّى هذه الحالة "كلوبن". ورغم أنها غير مألوفة في ℝ، فإنها ممكنة في الطوبولوجيا العامة عندما تُدرج الطوبولوجيا المجموعة ومتممتها ضمن المجموعات المفتوحة. هنا {a,b} مفتوحة بحكم تعريف T ومغلقة لأنها متمّم المجموعة المفتوحة X-{c,d}.
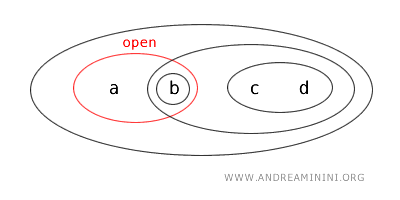
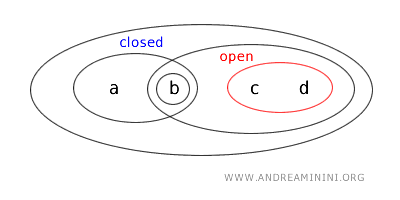
- {b,c} ليست مفتوحة ولا مغلقة لأنها لا تحقق شروط المجموعات المفتوحة، كما أنها ليست متمّمًا لأي مجموعة مفتوحة.
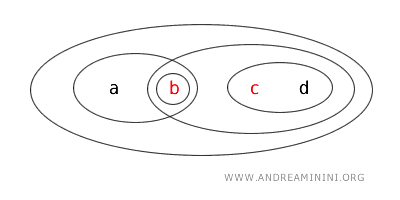
يتضح من هذا المثال أن المجموعات في الطوبولوجيا يمكن أن تكون مفتوحة أو مغلقة أو كلتيهما أو لا تنتمي إلى أي منهما.
خصائص المجموعة المغلقة
تُعرَّف المجموعة المغلقة بأنها متمّمة مجموعة مفتوحة، وتمتاز بالخصائص الأساسية الآتية:
- تُعد المجموعة الخالية (الرمز Ø) والفضاء بأكمله X مجموعتين مغلقتين بطبيعتهما.
- إن تقاطع أي عدد من المجموعات المغلقة يبقى مجموعة مغلقة.
- إن اتحاد عدد منتهٍ من المجموعات المغلقة يظل مجموعة مغلقة كذلك.
مثال:
في الطوبولوجيا القياسية للفضاء الإقليدي Rn تُعد كل نقطة مفردة مجموعة مغلقة.
فعلى خط الأعداد R1 إذا أخذنا نقطة مفردة n، فإن متمّمتها هي جميع النقاط في R1 باستثناء n.
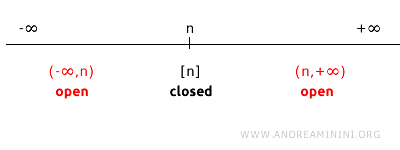
وبالتالي فإن متمّمة المجموعة {n} هي اتحاد المجالين المفتوحين: (-∞, n) ∪ (n, +∞).
وبما أن هذين المجالين (-∞, n) و (n, +∞) مفتوحان في الطوبولوجيا القياسية، فإن اتحادهما يشكّل مجموعة مفتوحة.
ومن ثمّ، وبما أن متمّمة {n} مجموعة مفتوحة، نستنتج أن {n} مجموعة مغلقة.
ومع ذلك، تجدر الإشارة إلى أن النقطة المفردة ليست بالضرورة مجموعة مغلقة في كل طوبولوجيا، فذلك رهنٌ بطبيعة البنية الطوبولوجية للفضاء. فمثلًا، إذا اعتُمِدت على R طوبولوجيا تُولَّد من المجالات المفتوحة (n, n + 1) لكل عدد صحيح n، فلن تُعد النقاط المفردة مجموعات مغلقة لأنها لا تضم حدودها المجاورة.
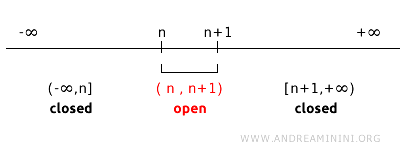
فعلى سبيل المثال، تُعد المجموعتان (1,2) و (2,3) مجموعتين مفتوحتين في هذه الطوبولوجيا. أما متمّمة المجال المفتوح (1,2) فهي المجموعة (-∞, 1] ∪ [2, +∞). وبالمثل، فإن متمّمة المجال المفتوح (2,3) هي المجموعة (-∞, 2] ∪ [3, +∞). ومن هنا يستحيل الحصول على متمّمة تُطابق المجموعة المفردة [2] ضمن هذه الطوبولوجيا. وبوجه عام، فإن متمّمة أي مجال مفتوح من الشكل (n, n+1) هي اتحاد مجموعتين مغلقتين: (-∞, n] ∪ [n+1, +∞). وعليه، لا تُعد النقاط المفردة مجموعات مغلقة في هذا السياق، مما يبيّن أن مفهوم الإغلاق يتحدد تبعًا للطوبولوجيا المُعتمدة على الفضاء.
حواشٍ
بعض الملاحظات التكميلية
- المجموعات المغلقة ونقاط التراص
تُعرَّف نقطة التراص لمجموعة ما بأنها نقطة يحتوي كل جوار لها، مهما صَغُر، عنصرًا آخر من عناصر المجموعة. وتمتاز المجموعات المغلقة بأنها تضم جميع نقاط تراصها، خلافًا للمجموعات المفتوحة التي قد لا تمتلك هذه الخاصية.مثال: لنأخذ المجال المغلق [0,1] على خط الأعداد. يحتوي هذا المجال جميع نقاط تراصه. فمثلًا، حول النقطة 0.5 يوجد دومًا جوار مفتوح يضم عددًا غير منتهٍ من النقاط الواقعة داخل [0,1]، مما يثبت أنها نقطة تراص.
![مثال لنقطة تراص داخل [0,1]](/data/andreaminininet/closed-set-example-limit-point-am-net-2024-1.gif)
وينطبق ذلك على جميع النقاط، بما في ذلك النقاط الحدّية. فالنقطة 0 تُعد نقطة تراص لأن كل جوار لها يضم عناصر من المجال، مثل 0.1 و 0.01 و 0.001 وغيرها.
![النقاط الحدّية للمجال [0,1] تُعد نقاط تراص أيضًا](/data/andreaminininet/closed-set-example-limit-point-am-net-2024-2.gif)
وبهذا يتبيّن أن كل نقطة في المجال المغلق [0,1] تحيط بها مجاورات مفتوحة تمتلئ بعناصر إضافية تنتمي للمجال نفسه. - المجموعة A مغلقة إذا وفقط إذا A = Cl(A)
في الفضاءات الطوبولوجية تُعد المجموعة \( A \) مغلقة إذا كانت مساوية لإغلاقها \( \text{Cl}(A) \). ويشمل الإغلاق جميع عناصر \( A \) بالإضافة إلى نقاط تراصها. فإذا كانت المجموعة تحتوي كل نقاط تراصها، فهي مجموعة مغلقة بالضرورة.
وما إلى ذلك.