الكرة المفتوحة

في الطوبولوجيا تُعد الكرة المفتوحة مفهوماً أساسياً. وهي ببساطة مجموعة النقاط التي تبعد مسافة أقل من مقدار معيّن عن نقطة ثابتة تُسمّى المركز (c). ويُطلق على هذا المقدار اسم نصف القطر (r). $$ B(c, r) = \{ x \in M \mid d(c, x) < r \} $$

تنتمي هذه الفكرة إلى فضاء متري \( M \)، أي فضاء مزوّد بدالة تُسمّى المترية. تقيس هذه الدالة المسافة بين أي نقطتين، وتسمح لنا ببناء طوبولوجيا واضحة لهذا الفضاء.

تتحدد الكرة المفتوحة عبر عنصرين فقط هما المركز ونصف القطر. ورغم بساطة التعريف فإن لهذا المفهوم دوراً محورياً في الطوبولوجيا.

وعندما نقول إن الكرة "مفتوحة" فهذا يعني أنه داخل كل كرة مفتوحة يمكن دائماً العثور على كرة مفتوحة أصغر تقع بكاملها داخل الكرة الأكبر. وهذا ما يعطي الفضاءات المترية بنيتها الطوبولوجية المرنة.

ملاحظة: تبقى خصائص الكرات المفتوحة ثابتة عند التكبير أو التصغير أو عند نقلها من مكان إلى آخر. فشكلها الطوبولوجي لا يتغير بمجرد تحريكها أو تغيير حجمها.

في المستوى الإقليدي \( R^2 \) مثلاً نستخدم المترية الإقليدية لقياس المسافة بين نقطتين، مثل النقطة p=(x,y) والنقطة c=(x₀,y₀) التي نختارها مركزاً.

$$ d(p,c) = \sqrt{(x-x_0)^2+(y-y_0)^2} $$

وتُعد الجوارات المفتوحة الطريقة التي نُعرّف بها البنية الطوبولوجية للمستوى. فهي أشبه بقطع الأساس التي تُبنى عليها الطوبولوجيا بأكملها.

الطوبولوجيا القياسية على المستوى \( R^2 \) تعتمد على جميع الكرات المفتوحة الممكنة في هذا الفضاء.

$$ B = \{ B(p, r) \ | \ p \in R^2, \ r > 0 \} $$

يشير p إلى نقطة من الشكل p=(x,y)، بينما يمثّل r نصف قطر الجوار المفتوح.

ورغم وجود طوبولوجيات أخرى ممكنة للمستوى فإن الطوبولوجيا القياسية تبقى الأكثر استخداماً وانتشاراً لسهولة التعامل معها وقابليتها للتطبيق في كثير من المجالات.

وفي كل كرة مفتوحة \( B(p,r) \) تكون كل نقطة \( q \in B(p,r) \) مركزاً لِكرة مفتوحة أصغر من النوع B(q,ε) تقع بالكامل داخل الكرة الأصلية. وهذا ما يجعل البنية الطوبولوجية متماسكة ومتدرجة.

$$ \forall \ q \in B(p,r) \ \exists \ \epsilon > 0 \ \text{بحيث} \ B(q,\epsilon) \subset B(p,r) $$

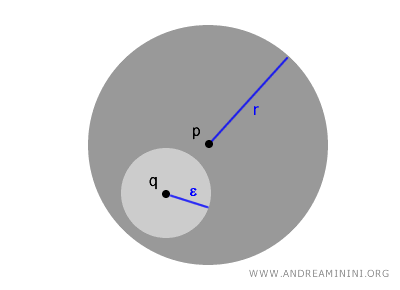
هذه الخاصية تتكرر في كل نقطة من نقاط الكرة المفتوحة، مما يمنح الطوبولوجيا بنية متجددة يمكن تحليلها نقطة بنقطة.