Bir Kümenin Sınırı
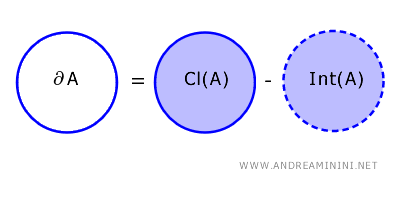
Bir topolojik uzay \( X \) içinde yer alan \( A \) altkümesinin sınırı, \( A \)'nın kapanışında bulunan ancak iç kısmına ait olmayan noktaların oluşturduğu kümedir. \[ \partial A = \text{Cl}(A) - \text{Int}(A) \]
Burada \( \text{Cl}(A) \), \( A \)'nın kapanışıdır. Yani yalnızca \( A \)'nın kendisini değil, aynı zamanda ona keyfi derecede yaklaşabilen tüm noktaları da içerir.
\( \text{Int}(A) \) ise \( A \)'nın içidir. Bu küme, çevresinde tamamen \( A \) içinde kalan bir açık komşuluğa sahip olan noktalardan oluşur.
Sınır kavramının önemli bir özelliği şudur: Bu kavram, kümenin kendisinden çok, üzerinde tanımlı olan topolojiye bağlıdır.
Dolayısıyla aynı küme, farklı bir topolojik yapı altında incelendiğinde farklı bir sınıra sahip olabilir.
Başka bir ifadeyle, bir \( A \) kümesinin sınırı; hem \( A \)'ya hem de tümleyeni \( X \setminus A \)'ya aynı anda yakın olan noktalardan oluşur.
Pratik Bir Örnek
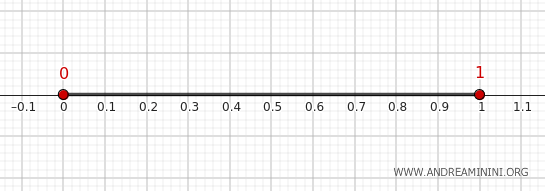
Standart topoloji ile donatılmış gerçek sayılar doğrusu \( \mathbb{R} \) üzerinde \[ A = (0,1) \] kümesini ele alalım.
Bu kümenin sınırını adım adım bulalım.
1] A Kümesinin Kapanışı
\( A \)'nın kapanışı \( \text{Cl}(A) \), kümenin tüm noktalarını ve yığılma noktalarını içerir.
\( A = (0,1) \) için bu kapanış, kapalı aralık olan \([0,1]\)'dir. Bunun nedeni, \((0,1)\) içindeki her noktanın bir yığılma noktası olması ve 0 ile 1 uç noktalarının da bu özelliği taşımasıdır.
\[ \text{Cl}(A) = [0,1] \]
2] A Kümesinin İçi
\( A \)'nın içi \( \text{Int}(A) \), tamamen \( A \) içinde kalan bir açık komşuluğa sahip noktaların kümesidir.
\( A = (0,1) \) için iç küme yine \((0,1)\)'dir. Çünkü bu aralıktaki her noktanın, tamamı bu aralık içinde kalan bir komşuluğu vardır.
\[ \text{Int}(A) = (0,1) \]
3] A Kümesinin Sınırı
Tanıma göre sınır, kapanış ile iç arasındaki farktır:
\[ \partial A = \text{Cl}(A) - \text{Int}(A) \]
Önceki sonuçları kullanırsak:
\[ \partial A = [0,1] - (0,1) = \{0,1\} \]
Yani standart topoloji altında \( A = (0,1) \) kümesinin sınırı \(\{0,1\}\) noktalarından oluşur.
Bu iki nokta, hem kümenin iç bölgesine hem de dışına komşu oldukları için sınırı temsil eder.
Sınır Teoremi
Bir topolojik uzay \( X \) içinde yer alan bir \( A \) altkümesinin sınırında bulunan bir \( x \) noktası, ancak ve ancak \( x \)'in her komşuluğu hem \( A \) ile hem de \( X - A \) ile kesişiyorsa \[ x \in \partial A \] olur.
Bu teorem, bir noktanın sınırda olup olmadığını anlamak için pratik bir ölçüt sunar.
Örnek
Yine \( \mathbb{R} \) üzerinde \( A = (0,1) \) kümesini ele alalım.
Bu küme için:
\[ \text{Cl}(A) = [0,1] \]
\[ \text{Int}(A) = (0,1) \]
Dolayısıyla sınır yalnızca 0 ve 1 noktalarından oluşur:
\[ \partial A = \{0,1\} \]
0 Noktası
0'ın herhangi bir komşuluğu \((0,1)\) aralığından noktalar içerir ve aynı zamanda 0'dan küçük noktaları da kapsar. Bu nedenle hem \( A \) ile hem de \( X-A \) ile kesişir.
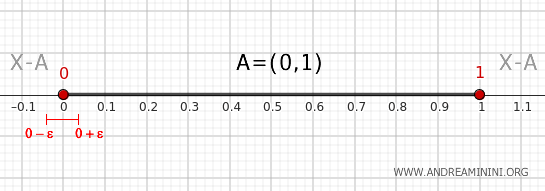
1 Noktası
1 için de benzer bir durum geçerlidir. Her komşuluk hem \((0,1)\) aralığından hem de 1'den büyük değerlerden noktalar içerir.
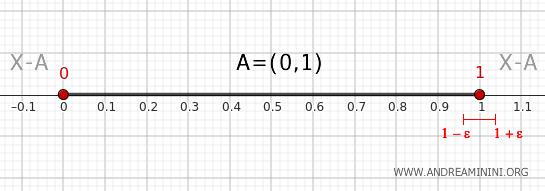
(0,1) İçindeki Bir Nokta
Örneğin 0.5 noktası için, yeterince küçük bir komşuluk tamamen \((0,1)\) içinde kalır ve \( X-A \) ile kesişmez. Bu nedenle 0.5 sınırda değildir.
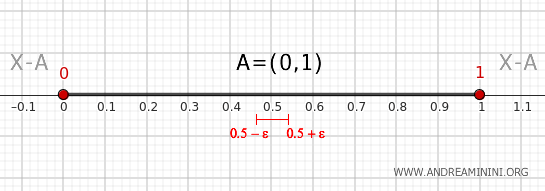
Bu gözlemler, sınırın neden yalnızca 0 ve 1 noktalarından oluştuğunu açıkça gösterir.
Notlar
Sınır kavramıyla ilgili bazı temel özellikler:
- \( \partial A \subseteq A \) ancak ve ancak \( A \) kapalıysa geçerlidir.
- \( A \) açıksa, sınır ile kümenin kesişimi boştur.
- Sınır ancak ve ancak \( A \) hem açık hem kapalıysa boştur.
- Sınır, \( A \)'nın kapanışı ile tümleyenin kapanışının kesişimidir. \[ \partial A = \text{Cl}(A) \cap \text{Cl}(X-A) \]
- Sınır kümesi her zaman kapalıdır.
Kapalı kümelerin kesişimi yine kapalıdır. Sınır, iki kapalı kümenin kesişimi olarak tanımlandığı için \[ \partial A = \text{Cl}(A) \cap \text{Cl}(X-A) \] her zaman kapalıdır.
- Sınır ile iç kümenin kesişimi boştur.
- Sınır ile iç kümenin birleşimi, kapanışı verir. \[ \partial A \cup \text{Int}(A) = \text{Cl}(A) \]
Bu özellikler, sınır kavramının topolojide neden bu kadar merkezi bir rol oynadığını net biçimde ortaya koyar.