Açık Bir Kümenin Standart Topolojisi

Standart topoloji, R üzerindeki her açık aralığı (a, b) (a < b koşuluyla) ve bu aralıkların sonlu ya da sonsuz birleşimlerini bir açık küme olarak kabul eder. Bu yaklaşım, gerçek sayı doğrusundaki açıklık kavramını matematiksel olarak kesin ve tutarlı hale getirir.

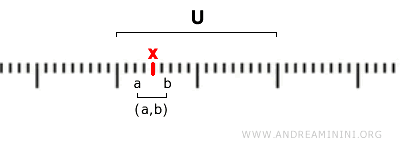
Bir U kümesinin açık olabilmesi için, U içindeki her x noktası için x’i içine alan bir (a, b) açık aralığı bulunmalı ve bu aralık tamamen U’nun içinde yer almalıdır.

$$ x \in (a,b) \subseteq U $$

Başka bir deyişle, U kümesini oluşturan her nokta, U’nun içinde kalan bir açık aralıkla çevrelenebilmelidir. Bu özellik, açık kümeleri kapalı kümelerden ayıran temel fikri oluşturur.

Bu tanım sayesinde standart topolojide şu kümeler açık kabul edilir:

• Açık aralıklar
  Gerçek sayı doğrusu üzerindeki temel açık kümeler, \( (a, b) \) şeklindeki açık aralıklardır. Bu aralıkların sonlu veya sonsuz birleşimleri de açık küme oluşturur.
• Küme işlemleri
  Açık kümeler, iki temel işlem altında kapanma özelliğine sahiptir:
  • Birleşim: Herhangi bir sayıda açık kümenin birleşimi yine açıktır.
  • Sonlu kesişim: Sonlu sayıda açık kümenin kesişimi de açıktır.

Standart topoloji, birçok farklı topoloji arasında en çok kullanılan ve analizin temelini oluşturan yapıdır. Bunun sebebi, yakınlık, süreklilik ve limit gibi kavramları sezgisel biçimde karşılamasıdır.

Not: Farklı topolojiler, farklı tabanlara dayanabilir. Bu durumda açık kümeler değişir ve ortaya bambaşka özelliklere sahip topolojik yapılar çıkabilir.

Örnek: Standart Taban

Gerçek sayı doğrusu üzerinde standart topolojinin tabanı, a < b olmak üzere tüm açık aralıklardan oluşur.

$$ B = \{ (a,b) \subset; R \ | \ a<b \} $$

Bu yapının önemli bir sonucu şudur: Açık bir kümedeki her nokta, o kümenin içinde tamamen kalan daha küçük bir açık aralıkla çevrelenebilir.

$$ \forall \ x \ \in U \ \exists \ \epsilon>0 \ | \ x \in (x-\epsilon, x+\epsilon) \subseteq U $$

Bu özellik, açıklık kavramının gerçek sayı doğrusu üzerinde nasıl işlediğini net biçimde gösterir.

Örnek 2: (0,1) Aralığı

Şimdi (0,1) aralığını ele alalım. Bu aralık uç noktalar olan 0 ve 1’i içermez ve standart topolojiye göre açık kabul edilir.

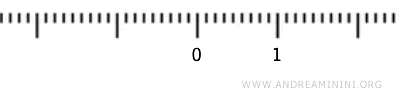
\( U \subset (0, 1) \) olmak üzere, her \( x \in U \) noktası için \( \mathbb{R} \) içinde bir \( (a, b) \) açık aralığı bulunur ve bu aralığın \( (0,1) \) ile kesişimi \( U \)’nun içinde kalır. Bu nedenle (0,1) toplamsal işlemler altında açık kümelerden oluşan bir topolojik uzay yapısını korur.

Örneğin \( (0.1, 0.5) \), \( (0.2, 0.9) \) ya da bunların birleşimi olan \( (0.1, 0.5) \cup (0.6, 0.8) \), bu aralığın türetilmiş topolojisinde açık kümelerdir.

Örnek 3: Sonlu Bir Küme

Şimdi X={1,2,3} gibi sonlu bir kümeyi düşünelim. Standart topolojide açık kümelerin temeli açık aralıklar olduğu için, bu tanım doğrudan X üzerinde uygulanamaz.

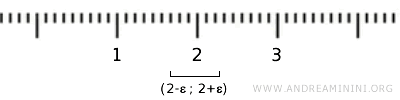
Bu durumda X, standart topolojiyle anlamlı bir yapı oluşturmaz. Bunun yerine sonlu kümeler için her alt kümenin açık kabul edildiği ayrık topoloji daha kullanışlıdır.

Bu örnekler, standart topolojinin neden güçlü ve yaygın bir araç olduğunu gösterir. Gerçek sayılar üzerinde çalışan analiz, cebir ve topoloji konularında temel referans olmasının sebebi budur.