Normal topolojik uzay

Bir topolojik uzay $ X $, aşağıdaki iki koşulu sağlıyorsa normal olarak adlandırılır:

Tekil noktalar kapalı kümelerdir
Yani her $ x \in X $ noktası için $\{x\}$ kümesi, verilen topolojide kapalıdır.
Birbirinden ayrık iki kapalı küme, ayrık açık kümelerle ayrılabilir
Eğer $ A $ ve $ B $ kapalı kümeleri kesişmiyorsa (yani $ A \cap B = \emptyset $), o hâlde aşağıdaki koşulları sağlayan iki açık küme $ U $ ve $ V $ bulunur:
- $ A \subset U $
- $ B \subset V $
- $ U \cap V = \emptyset $

Normal uzay kavramı, topolojide kümeleri birbirinden “ayırabilme” yeteneğini ifade eder. Böyle uzaylarda, iki ayrık kapalı küme her zaman birbirine değmeyen iki ayrı açık küme içinde bulunabilir.

Bu özellik, noktaları veya kapalı kümeleri ayıran sürekli fonksiyonlar tanımlamak açısından çok önemlidir. Özellikle Urysohn ayrım teoremi gibi temel sonuçların temelini oluşturur.

Bir örnek üzerinden açıklama
Ek bilgiler

Bir örnek üzerinden açıklama

Standart topolojiye sahip $ X = \mathbb{R} $ uzayını düşünelim. Bu topoloji, $ (a, b) $ biçimindeki açık aralıklarla tanımlanır.

$ \mathbb{R} $ üzerinde iki ayrık kapalı küme seçelim:

$ A = \{0\} $: tek bir noktadan oluşan bir küme.
$ B = [2, 3] $: kapalı bir aralık.

Her iki küme de $ \mathbb{R} $’nin standart topolojisinde kapalıdır ve ortak noktaları olmadığından ayrık kümelerdir.

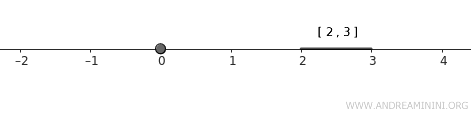
örnek

Not. $ A $ kümesi yalnızca bir noktadan oluştuğu ve çevresindeki noktaları içermediği için kapalıdır. $ B $ ise uç noktalarını da içeren bir aralık olduğundan kapalı bir kümedir.

Şimdi bu kümeleri kapsayan iki ayrık açık küme bulalım.

Birinci açık küme $ U = (-1, 1) $ olsun; bu küme $ A = \{0\} $’ı kapsar.

$$ A \subset U = (-1,1) $$

İkinci olarak $ B = [2,3] $ için $ V = (1, 4) $ seçelim; bu açık küme $ B $’yi tamamen kapsar.

$$ B \subset V = (1,4) $$

Bu durumda $ U $ ve $ V $ kümeleri kesişmediğinden ($ U \cap V = \emptyset $) ayrık açık kümelerdir.

Dolayısıyla standart topolojiye sahip $ \mathbb{R} $ uzayı normal bir topolojik uzaydır.

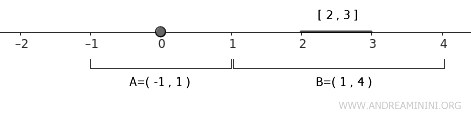
örnek

Aynı mantık, herhangi iki ayrık kapalı küme için de geçerlidir: onları kapsayan ayrık açık kümeler her zaman bulunabilir. Bu nedenle, gerçek sayı doğrusu $ X = \mathbb{R} $ normal bir topolojik uzaydır.

Ek bilgiler

Normal topolojik uzaylarla ilgili birkaç önemli nokta:

Standart topolojiye sahip $ \mathbb{R} $ normaldir
Bu uzay yalnızca düzenlilik koşulunu (bir noktayı kapalı bir kümeden ayrık açık kümelerle ayırabilmeyi) sağlamakla kalmaz, aynı zamanda daha güçlü olan normal olma koşulunu da karşılar.
Her metrik uzay normaldir
Noktalar arasındaki mesafeleri tanımlayan bir metrik varsa, bu uzay otomatik olarak normaldir.
Her normal uzay düzgündür
Yani normal olma, düzenlilikten (regularlikten) daha güçlü bir ayrılma özelliğidir.

Sonuç olarak, normal topolojik uzay kavramı, topolojideki ayrılma aksiyomlarının en önemli halkalarından biridir.