Topolojide Bağlantılılık

Topolojide bir uzay, ayrık açık kümelerden oluşmuyorsa bağlantılı kabul edilir. Yani, uzayın içindeki herhangi iki nokta, sınırların dışına çıkmadan bir yol aracılığıyla birbirine bağlanabiliyorsa bu uzay bağlantılıdır.

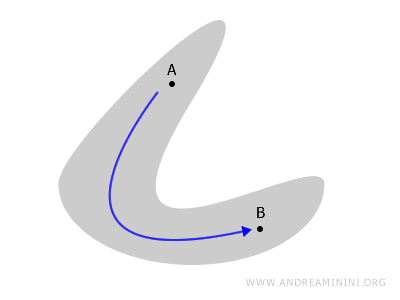
Bağlantılılık, bir topolojik uzayın parçalarının nasıl bir bütün oluşturduğunu veya birbirinden nasıl ayrıldığını anlatır.

Bu, açık kümeler cinsinden tanımlandığı için topolojik bir özelliktir.

Bu kavram, topolojide süreklilik kadar temel bir öneme sahiptir.

Bağlantılılık, matematiğin birçok alanında merkezi bir rol oynar; çünkü uzayın yapısını ve farklı bileşenler arasındaki ilişkileri anlamamıza yardımcı olur. Örneğin, topolojik uzayların sınıflandırılması ve incelenmesinde belirleyici bir araçtır.

Somut Bir Örnek

Bir uzay - ister düzlemsel bir şekil ister çokyüzlü olsun - eğer içindeki herhangi iki nokta A ve B, sınırların dışına çıkmadan sürekli bir yol ile birbirine bağlanabiliyorsa, o uzay bağlantılıdır.

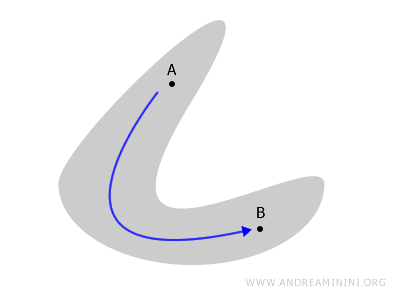
Buna karşılık, eğer uzayın bazı bölümleri birbirinden kopmuşsa, bu durumda uzay bağlantısızdır (yani bir ayrık uzay söz konusudur).

Örneğin, bu durumda uzay iki ayrı parçaya bölünmüştür ve A ile B noktalarını bağlayacak herhangi bir yolun uzayın dışına çıkması gerekir.

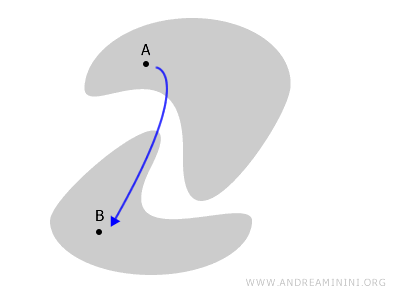
Bağlantısız uzay kavramını, başka bir somut örnek üzerinden biraz daha derinleştirelim.

Bir uzay ne zaman bağlantısızdır?

Bağlantısız bir uzayı gözümüzde canlandırmanın en kolay yolu, aynı binada bulunan ancak bir duvarla ayrılmış iki oda düşünmektir. Bu odalar, sınırlarını (duvarlarını) içermeyen, birbirinden kopuk açık kümeleri temsil eder.

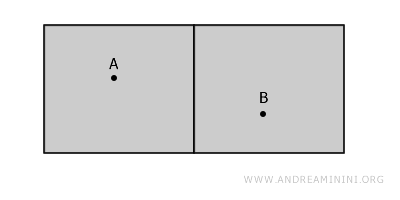
Odalar yan yana görünse de bağlantılı değildir; çünkü A noktasından B noktasına ulaşmak için mutlaka duvardan geçmek gerekir ve bu, tanımlanan uzayın dışında kalır.

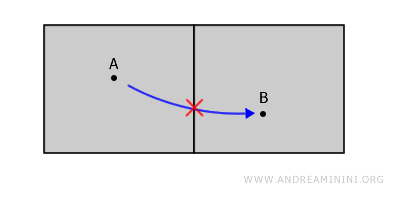
Kısacası, sınırların hiçbir zaman açık kümelerin parçası olmadığını unutmamak gerekir.

Yerel Bağlantılılık

Bir uzayın yerel bağlantılı olması, uzaydaki her noktanın, bağlantılı bir açık altkümeye ait olması demektir. Yani, uzay ayrık kümelerden oluşsa bile her noktanın içinde bulunduğu küçük bir çevre bağlantılıdır.

Örneğin, bir binanın içindeki iki ayrı odayı temsil eden ayrık açık kümeleri düşünelim.

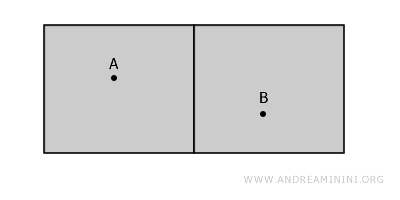
Bu uzay bağlantısızdır; çünkü A ve B noktalarını birbirine bağlamak için duvarlardan geçmek gerekir.

Ancak A noktasının çevresinde, tüm noktaların birbirine bağlı olduğu bir altküme bulunur. Bu, o noktada yerel bağlantılılık olduğunu gösterir.

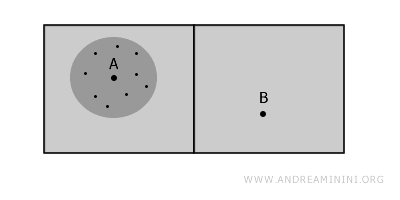
Aynı durum B noktası için de geçerlidir: o da yerel bağlantılıdır.

Bağlantılılık Türleri

Bağlantılılık farklı biçimlerde karşımıza çıkar. En yaygın iki tür şunlardır:

• Topolojik bağlantılılık
  Bir topolojik uzay $ X $, eğer boş olmayan ve birbirinden ayrık iki açık kümenin birleşimi tüm uzayı oluşturamıyorsa bağlantılı olarak adlandırılır. Başka bir ifadeyle, bu uzayı iki bağımsız bölgeye “ayırmanın” bir yolu yoktur.

  Örnek. $(-1, 1)$ aralığı bağlantılı bir uzaydır. Buna karşılık $(-1, 0) \cup (0, 1)$ aralığı bağlantısızdır; çünkü $(-1, 0)$ ve $(0, 1)$ kümeleri hem boş değildir hem de ayrık olup birleşimleri uzayın tamamını kapsar.
  Dolayısıyla bu iki küme uzayın bir ayrımını oluşturur.

• Yol bağlantılılık (ya da yay bağlantılılık)
  Bir topolojik uzay, içindeki herhangi iki nokta A ve B arasında tamamen uzayın içinde kalan sürekli bir yol çizilebiliyorsa yol bağlantılı olarak adlandırılır. Her yol bağlantılı uzay aynı zamanda bağlantılıdır; ancak her bağlantılı uzay mutlaka yol bağlantılı olmak zorunda değildir.

  Örneğin, düzlem üzerindeki kapalı bir şekli düşünelim. Şeklin içindeki herhangi iki nokta A ve B arasında kalemi kaldırmadan ve şeklin dışına çıkmadan sürekli bir eğri çizebiliriz.
  
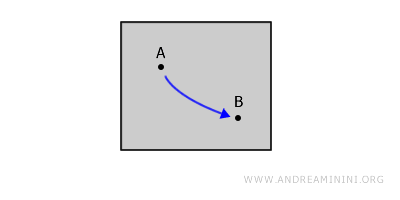
  Yay bağlantılılık ile yol bağlantılılık arasındaki fark.  Yay bağlantılılık, yol bağlantılılığa benzerdir; ancak burada çizilen yol bire-bir olmalıdır, yani kendi üzerine dönmez ve aynı noktadan iki kez geçmez.

• Basit Bağlantılılık
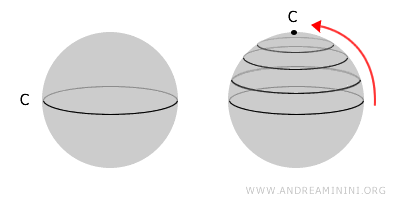
  Bir uzay, içindeki her kapalı halkanın bir noktaya küçültülebilmesi durumunda basit bağlantılıdır. Bu, uzayın içinde boşluk olmadığını gösterir. Basit bağlantılı bir uzay her zaman bağlantılıdır; ancak bağlantılı her uzay basit bağlantılı değildir. Daha teknik bir ifadeyle, basit bağlantılı bir uzayda her halka bir noktaya homotopiktir.

  Örneğin, bir küre basit bağlantılıdır; çünkü yüzeyindeki herhangi bir halka bir noktaya indirgenebilir. Buna karşılık, iç kısmında delik barındıran bir torus (simit yüzeyi) her halkayı bir noktaya küçültemez. Bu da onun bağlantılı ama basit bağlantılı olmadığını gösterir.
  
  
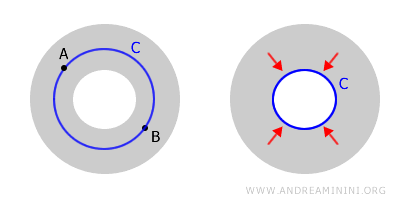
  Bu tür bir uzay, bağlantılı ama basit bağlantılı olmadığı için çoklu bağlantılı olarak adlandırılır. Halka biçimli bir uzay bu tür bağlantılılığa klasik bir örnektir.

Notlar

Son olarak birkaç gözlem:

• Gerçel sayılar kümesinde bağlantılı olan tek kümeler aralıklardır.