Bir kümenin kapanışı

Bir topolojik uzay \( X \) içinde verilen \( A \) kümesinin kapanışı, \( A \)’yı kapsayan tüm kapalı kümelerin kesişimi olarak tanımlanır ve \( \text{Cl}(A) \) ile gösterilir.

Bu tanımın özü şudur: kapanış, \( A \)’yı tamamen içine alan en küçük kapalı kümedir.

Gerçekten de, \( A \)’yı içeren hiçbir kapalı küme, \( A \)’nın kapanışından daha dar olamaz.

Not: Bu özellik doğrudan tanımdan gelir. Kapanış, \( A \)’yı içeren tüm kapalı kümelerin kesişimi olduğundan, sezgisel olarak \( A \)’nın etrafındaki en sıkı kapalı “kabuk”tur. Yalnızca, \( A \)’yı kapsayan her kapalı kümede ortak olan noktaları içerir.

Biçimsel olarak, \( A \) kümesinin kapanışı şu şekilde yazılır:

$$ \text{Cl}(A) = \bigcap \{ C \subseteq X : A \subseteq C \text{ ve } C, X \text{’te kapalıdır} \} $$

Burada \( \bigcap \) sembolü, \( A \)’yı içeren tüm kapalı kümelerin kesişimini ifade eder.

\( A \)’nın kapanışı, kümenin kendisini ve ayrıca \( X \) içindeki tüm limit (birikim) noktalarını kapsar.

Not: Önemli bir nokta şudur: bir kümenin kapanışı, büyük ölçüde içinde bulunduğu topolojik uzayın yapısına bağlıdır. Aynı küme, farklı topolojiler altında farklı kapanışlara sahip olabilir.

Açıklayıcı bir örnek

Gerçek sayılar kümesi \( \mathbb{R} \) üzerinde tanımlı standart topoloji altında \( A = (0,1) \) kümesini ele alalım.

Bu küme, 0 ile 1 arasındaki tüm gerçek sayıları içerir, ancak uç noktalar olan 0 ve 1 bu kümeye dahil değildir.

Bu durumda \( A \)’nın kapanışı, uç noktaların da eklendiği

$$ \text{Cl}(A) = [0,1] $$

kümesidir.

Bu kapanış, açık aralık \( (0,1) \)’i ve sınırda bulunan 0 ile 1 noktalarını, yani kümenin birikim noktalarını birlikte içerir.

Not: Standart topolojide kapalı kümeler, tüm limit noktalarını içeren kümelerdir. Bir limit noktası, etrafındaki her komşuluğun kümeden farklı en az bir nokta içermesiyle tanımlanır. Örneğin $$ [0,2] \cap [-1,1] = [0,1] $$ olur ve \( (0,1) \) kümesini kapsayan bundan daha küçük bir kapalı aralık yoktur.

Örnek 2

Şimdi yine standart topoloji altında \( A = [0,1) \) kümesini inceleyelim.

Bu küme 0 noktasını içerir, ancak 1 noktasını içermez. Yani soldan kapalı, sağdan açık bir aralıktır.

Bu durumda da kapanış değişmez:

$$ \text{Cl}(A) = [0,1] $$

Bunun nedeni, 0’ın zaten kümenin içinde yer alması, 1’in ise kümenin dışında kalan bir limit noktası olmasıdır.

Dolayısıyla kapanış, eksik olan sağ uç noktayı da ekleyerek \( A \)’yı içeren en küçük kapalı küme olan \( [0,1] \)’i verir.

Not: Bu örnek, kapanışın bir kümenin tüm birikim noktalarını kapsadığı fikrini net biçimde ortaya koyar. Yine $$ [0,2] \cap [-1,1] = [0,1] $$ eşitliği bu ilkenin bir sonucudur.

Örnek 3

Aynı \( A = [0,1) \) kümesini bu kez ayrık topoloji altında ele alalım.

Ayrık topolojide, uzayın her altkümesi hem açık hem de kapalıdır.

  • Açık küme
    Ayrık topolojide \( X \)’in her altkümesi açıktır. Bu nedenle \( A \subset X \) olduğundan \( A \) da açıktır.
  • Kapalı küme
    Her altkümeye ait tümleyen de açık olduğundan, her altküme aynı zamanda kapalıdır. Örneğin \( X/A \) açık olduğu için \( A \) kapalıdır.

Hem açık hem kapalı olan bu tür kümelere topolojide “clopen” kümeler denir.

Bu durumda kapanış son derece basittir:

$$ \text{Cl}(A) = [0,1) $$

Yani kümenin kapanışı, bizzat kendisidir. Çünkü onu “tamamlamak” için yeni bir noktaya ihtiyaç yoktur.

Not: Bu örnek, topoloji seçiminin kapanış kavramını ne kadar güçlü biçimde etkilediğini açıkça gösterir.

Örnek 4

\( X = \{a, b, c\} \) noktalarından oluşan ve ayrık topoloji ile donatılmış bir topolojik uzay düşünelim.

Ayrık topolojide \( X \)’in tüm altkümeleri açıktır:

  • \( \emptyset \) ve \( \{a, b, c\} \) tanım gereği açıktır.
  • Tekil kümeler \( \{a\} \), \( \{b\} \), \( \{c\} \) açıktır.
  • Bunların tüm birleşimleri, örneğin \( \{a, b\} \), \( \{a, c\} \), \( \{b, c\} \)  de açıktır.

Aynı gerekçeyle bu kümelerin tümü kapalıdır.

Dolayısıyla ayrık topolojide her küme hem açık hem kapalıdır.

Bu uzayda \( A = \{b, c\} \) kümesini ele alalım. \( A \) açıktır ve tümleyeni \( X/A = \{a\} \) açık olduğu için aynı zamanda kapalıdır.

Kapanış tanımı gereği, \( A \)’yı içeren kapalı kümelerin kesişimi alınır ve ek bir noktaya gerek kalmaz:

\[ Cl(A) = \{b, c\} \]

Bu topolojide tüm kümeler zaten kapalı olduğu için ayrıca bir kapatma işlemine ihtiyaç duyulmaz.

Not: Hızlı bir kontrol olarak, \( A \)’yı içeren kapalı kümeler yalnızca \( \{b, c\} \) ve \( \{a,b,c\} \)’dir. Bunların kesişimi $$ Cl(A) = \{b,c\} \cap \{a,b,c\} = \{b, c\} $$ olduğundan sonuç doğrudan \( Cl(A) = A \) çıkar.

Bir Kümenin Kapanış Teoremi

Bir topolojik uzay \( X \) içinde, bir \( y \) noktası, bir \( S \) altkümesinin kapanışına, yani \( \text{Cl}(S) \)’ye, ancak ve ancak \( y \)’yi içeren her açık küme \( U \), \( S \) ile boş olmayan bir kesişime sahipse aittir: \( y \in \text{Cl}(S) \iff \forall \ U \text{ açık ve } y \in U \text{ ise } U \cap S \neq \emptyset \).

Bu ifade şu fikri netleştirir: Bir nokta, bir kümenin kapanışında yer alıyorsa, onu çevreleyen hiçbir açık küme o kümeden tamamen kopuk olamaz.

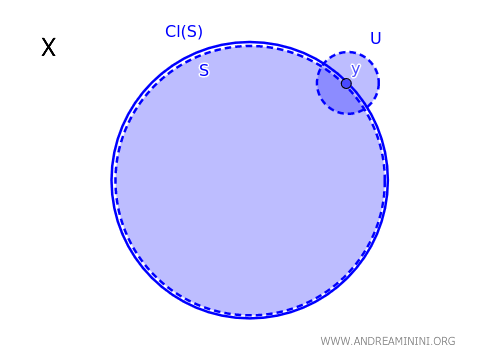
bir noktanın bir kümenin kapanışına ait olmasını açık kümeler aracılığıyla gösteren şema

Kapanış teoremi, bir noktanın bir kümenin kapanışına ait olup olmadığını kontrol etmek için hem sezgisel hem de güçlü bir ölçüt sunar.

İspat

  • Gerekli koşul: Eğer \( y \), \( S \)’nin kapanışında yer alıyorsa, tanım gereği \( y \)’yi içeren her açık küme \( S \) ile kesişmek zorundadır. Kapanış, yalnızca kümenin kendi noktalarını değil, aynı zamanda tüm limit (birikim) noktalarını da kapsar. Bir limit noktasının ayırt edici özelliği, onu içeren her açık komşuluğun kümenin kendisiyle kesişmesidir.
  • Yeterli koşul: Tersine, \( y \)’yi içeren her açık küme \( S \) ile kesişiyorsa, bu durumda \( y \) ya doğrudan \( S \)’nin bir elemanıdır ya da \( S \)’nin bir limit noktasıdır. Her iki durumda da \( y \), zorunlu olarak \( S \)’nin kapanışına aittir. Başka bir deyişle, \( y \)’ye \( S \) içinden keyfi derecede yaklaşılabiliyorsa, \( y \) kapanışta yer alır.

Not: Bu teorem, genel topolojide temel bir araçtır. Açık kümeler ile kapanış kavramı arasında doğrudan bir bağ kurar. Süreklilik, dizilerin ve ağların (netlerin) yakınsaklığı gibi pek çok önemli topolojik kavramın anlaşılmasında merkezi bir rol oynar.

Örnek

Gerçek sayılar kümesi \( \mathbb{R} \)’nin standart topolojisi altında \( A = (0,2) \) kümesini ele alalım. Bu küme, 0 ile 2 arasındaki açık aralığı temsil eder.

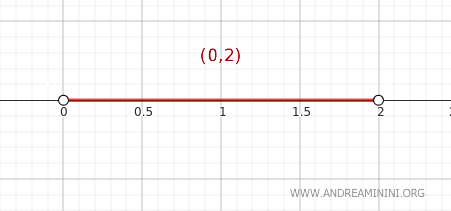
gerçek sayılar doğrusu üzerinde açık bir aralığın kapanışını gösteren görsel örnek

Kapanış teoremini kullanarak, bir noktanın \( A \)’nın kapanışına ait olup olmadığını inceleyelim.

Örneğin \( y = 2 \) noktasını ele alalım.

Teoreme göre, \( y \in \text{Cl}(A) \) olması için, \( y \)’yi içeren her açık kümenin \( A \) ile kesişmesi gerekir.

  1. \( y \)’yi içeren açık kümelerin incelenmesi: \( y = 2 \)’yi kapsayan herhangi bir açık aralık seçildiğinde, örneğin \( (1.9,2.1) \), \( (1.95,2.05) \), \( (1.99,2.01) \) gibi, bu aralıkların her birinin \( A = (0,2) \) kümesinden noktalar içerdiği görülür. Örneğin 1.95 ve 1.99 hem bu açık aralıklara hem de \( A \)’ya aittir.
  2. Kesişimin doğrulanması: \( y = 2 \)’yi içeren her açık küme \( A \) ile kesiştiğinden, teorem uyarınca \( y = 2 \)’nin \( \text{Cl}(A) \)’ya ait olduğu sonucuna ulaşılır.

Dolayısıyla \( y = 2 \) noktası, onu içeren her açık küme \( A \) ile kesiştiği için kapanışta yer alır:

$$ y \in \text{Cl}(A) $$

Nitekim bu durumda \( A \)’nın kapanışı, kapalı aralık olan \( \text{Cl}(A) = [0,2] \)’dir ve bu aralık 2 noktasını da kapsar.

Topolojik Uzaylarda Kapanışın Temel Özellikleri

Bir kümenin kapanışı, topolojik yapı içinde pek çok temel özellikle ilişkilidir. Aşağıda, kapanış kavramının en önemli sonuçları ve iç kısım (interior) işlemiyle olan ilişkileri özetlenmiştir.

Temel Gözlemler

Kapanış kavramıyla ilgili aşağıdaki özellikler, topoloji literatüründe standart ve temel sonuçlar olarak kabul edilir:

Devamı gelecek.

 
 
Please feel free to point out any errors or typos, or share suggestions to improve these notes.

FacebookTwitterLinkedinLinkedin

Topoloji

Alıştırmalar