Topolojide Homeomorfizmalar

Homeomorfizma, topoloji alanında, hem kendisi hem de tersi sürekli olan birebir (biyektif) bir dönüşümü ifade eder.

Bu tür bir dönüşüm, bir uzayı “koparmadan” ya da “yapıştırmadan” başka bir uzaya çevirmeyi ve ardından orijinal haline geri döndürmeyi mümkün kılar.

Daha sade bir ifadeyle, homeomorfizma bir uzayın şeklini diğerine nazikçe dönüştürür; süreçte hiçbir yırtılma ya da ekleme olmaz.

Örneğin, bir kulplu kahve fincanı ile bir donut (torus) topolojide homeomorfiktir. Çünkü biri sürekli biçimde diğerine dönüştürülebilir ve bu işlem tersine de yapılabilir.

Topolojik açıdan bu iki şekil eşdeğerdir; çünkü her ikisinde de yalnızca bir “delik” bulunur: donutun ortasındaki boşluk ile fincanın kulp kısmındaki boşluk aynı topolojik özelliği paylaşır. Fincanı kulpunun etrafında yumuşakça biçimlendirerek bir donut haline getirebilirsiniz.

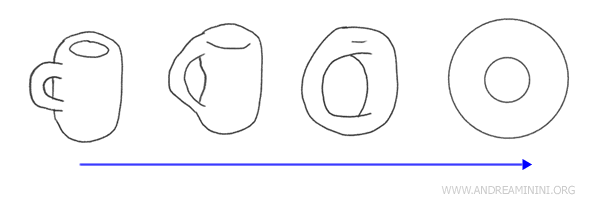
İki topolojik uzay bir homeomorfizma ile birbirine bağlanıyorsa, bu uzaylara “homeomorfik uzaylar” denir. Yani topolojik bakımdan özdeştirler; geometrik görünümleri farklı olsa da yapısal olarak aynıdırlar.

Bir homeomorfizmanın temel özellikleri

Homeomorfizmayı tanımlayan başlıca özellikler şunlardır:

• Biyektif fonksiyon
  İki uzayın elemanları arasında bire bir ve örten bir ilişki kurar. Her eleman yalnızca tek bir karşılığa sahiptir ve bu eşleme tersine çevrilebilir.
• Süreklilik
  Homeomorfizma doğası gereği süreklidir: girişteki küçük değişimler çıkışta da küçük değişimlere karşılık gelir.
• Sürekli ters fonksiyon
  Ters fonksiyonun da sürekli olması gerekir. Böylece dönüşümün sürekliliği bozulmadan geri alınması sağlanır.
• Topolojik özelliklerin korunması
  Süreklilik, bağlantılılık ve kompaktlık gibi temel topolojik özellikler korunur. Dolayısıyla, başlangıçtaki uzayın iç yapısı dönüştürülmüş uzayda da aynen kalır.

Özetle, bir homeomorfizma \(X\) ve \(Y\) topolojik uzayları arasında tanımlanan, hem kendisi hem de tersi sürekli olan bir fonksiyondur. Bu özellik, her iki uzayın topolojik niteliklerinin korunmasını sağlar.

Kısaca, homeomorfizma bir uzayı yırtmadan veya yapıştırmadan başka bir uzaya “yeniden biçimlendirme” yöntemidir. İki şekil ya da uzay arasında kusursuz bir “topolojik eşdeğerlik”tir.

Topolojide süreklilik tanımı şu şekildedir:

İki topolojik uzay \(X\) ve \(Y\) verildiğinde, \(f: X \to Y\) fonksiyonu, \(Y\)’deki her açık küme \(V\) için ön görüntüsü \(f^{-1}(V)\)’nin \(X\)’te açık olması durumunda sürekli kabul edilir.

Başka bir ifadeyle, topolojide sürekli bir fonksiyon, noktaları bir uzaydan diğerine taşırken açık kümelerin yapısını korur.

Dolayısıyla, topolojideki süreklilik kavramı, matematiksel analizde kullanılan süreklilikten daha soyut ve geneldir.

Not: Analizde süreklilik, noktalar arasındaki mesafeye dayanarak tanımlanır. Oysa topolojide, mesafe kavramına gerek kalmadan, açık kümelerin yapısı temel alınır.

Uygulamalı bir örnek

Homeomorfizma ve süreklilik kavramlarını açık kümeler üzerinden basit bir örnekle açıklayalım.

İki topolojik uzay düşünelim: \(X = \{a, b, c, d\}\) ve \(Y = \{1, 2\}\).

• \(X\) uzayındaki açık kümeler: \(\{\}, \{a\}, \{a, b\}, \{a, b, c, d\}\).
• \(Y\) uzayındaki açık kümeler: \(\{\}, \{1\}, \{1, 2\}\).

\(f: X \rightarrow Y\) fonksiyonu, \(Y\)’deki her açık kümenin ön görüntüsü \(X\)’te açık bir küme ise süreklidir.

Fonksiyonu şu şekilde tanımlayalım:

\(f(a) = 1\), \(f(b) = 1\), \(f(c) = 2\), \(f(d) = 2\).

Görselleştirmeyi kolaylaştırmak için \(f\) fonksiyonunu ve topolojik uzayları, açık kümeleri daire içine alarak temsil edelim.

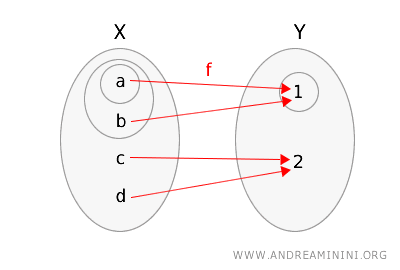
Şimdi topolojik süreklilik koşulunun sağlanıp sağlanmadığını inceleyelim.

• \(Y\)’deki açık küme \(\{1\}\)’i alırsak, ön görüntüsü \(f^{-1}(\{1\}) = \{a, b\}\)’dir ve bu \(X\)’te açık bir kümedir.
• \(Y\)’deki açık küme \(\{1, 2\}\)’yi alırsak, ön görüntüsü \(f^{-1}(\{1, 2\}) = \{a, b, c, d\}\)’dir ve bu da \(X\)’te açıktır.

\(Y\)’deki her açık kümenin ön görüntüsü \(X\)’te açık olduğundan, bu fonksiyon sürekildir.

Not: Boş küme, tanımı gereği her topolojik uzayda açık olduğundan ayrıca değerlendirmeye gerek yoktur.

Şimdi şu şekilde tanımlanan başka bir fonksiyonu ele alalım: \(g: X \rightarrow Y\)

\(g(a) = 1\), \(g(b) = 1\), \(g(c) = 1\), \(g(d) = 2\).

Bu durumda da \(g\) fonksiyonunu ve uzayları açık kümeleri daire içine alarak gösterelim.

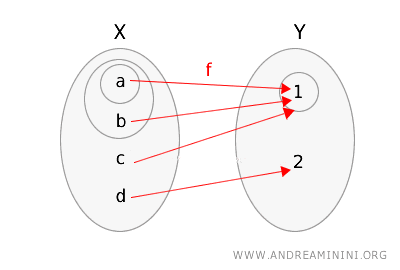
Şimdi topolojik süreklilik koşulunu sağlayıp sağlamadığına bakalım.

• \(Y\)’deki açık küme \(\{1\}\)’i alırsak, ön görüntüsü \(g^{-1}(\{1\}) = \{a, b, c\}\)’dür ve bu açık bir küme değildir.

\(Y\)’deki en az bir açık kümenin ön görüntüsü \(X\)’te açık olmadığından, \(g\) fonksiyonu sürekli değildir.

Not: Özetle, bir fonksiyonun sürekli olabilmesi için hedef uzaydaki (\(Y\)) her açık kümenin ön görüntüsünün \(X\)’te de açık olması gerekir. İlk durumda \(f\) fonksiyonu bu koşulu her zaman sağladığı için sürekildir. Buna karşılık, \(g\) fonksiyonu bu koşulu tüm açık kümeler için sağlamadığından sürekli değildir.

Homeomorfizmanın tanımı

İki topolojik uzay \( X \) ve \( Y \) verilsin. \( f: X \to Y \) birebir bir fonksiyon ve onun tersi \( f^{-1}: Y \to X \) olsun. Eğer hem \( f \) hem de \( f^{-1} \) sürekli ise, bu durumda \( f \)’ye homeomorfizma denir ve \( X \) ile \( Y \) homeomorfik uzaylar olarak adlandırılır, yani \( X \cong Y \).

Homeomorfik uzaylara aynı zamanda topolojik olarak eşdeğer uzaylar da denir.

Bu ne anlama gelir?

İki uzayın homeomorfik ya da topolojik olarak eşdeğer olması, topolojik bakış açısından aynı temel yapıya sahip olmaları demektir. Başka bir ifadeyle, geometrik biçimleri farklı olsa da, topolojik olarak aynı “öz”ü paylaşırlar.

Bir homeomorfizmanın tanımı üç temel koşula dayanır:

1. Biyektiflik: \( f: X \to Y \) fonksiyonu hem birebir hem de örten olmalıdır. Yani \( X \)’teki her nokta \( Y \)’de tam olarak bir noktaya karşılık gelir ve bu eşleme tersine çevrilebilir.
2. \( f \)’nin sürekliliği: \( f \) fonksiyonu, \( Y \)’deki her açık kümenin ön görüntüsü \( X \)’te açık olduğunda süreklidir.
3. \( f^{-1} \)’in sürekliliği: Ters fonksiyon \( f^{-1}: Y \to X \) da sürekli olmalıdır; yani \( X \)’teki her açık kümenin görüntüsü \( Y \)’de açık olmalıdır.

Örnek: Bir kâğıt parçasını rulo yaparak bir silindir oluşturduğunuzu düşünün. Silindir ile düz kâğıt homeomorfiktir; çünkü biri diğerine herhangi bir kesme veya yapıştırma işlemi olmadan, yalnızca sarma ya da açma yoluyla dönüştürülebilir. Geometrik biçim değişse de topolojik yapı - yani açık kümelerin düzeni - değişmeden kalır.

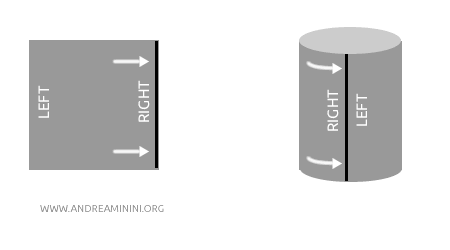
Şu noktayı vurgulamak gerekir: Biyektif bir fonksiyon \( f \)’nin sürekli olması, ters fonksiyonun \( f^{-1} \)’in de sürekli olacağını garanti etmez. Bu ancak \( f \) aynı zamanda açık bir fonksiyon olduğunda geçerlidir.

Dolayısıyla, sürekli ve biyektif bir fonksiyon, eğer tersi sürekli değilse, bir homeomorfizma değildir.

Topolojide, \( f: X \rightarrow Y \) fonksiyonu, \( Y \)’deki her açık kümenin ön görüntüsü \( X \)’te açık olduğunda sürekli kabul edilir.

Ancak bu durum, \( X \)’teki her açık kümenin görüntüsünün \( Y \)’de de açık olacağı anlamına gelmez.

\( f^{-1} \)’in sürekli olabilmesi için \( f \)’nin yalnızca sürekli ve biyektif değil, aynı zamanda açık bir fonksiyon olması gerekir.

Örnek

Aşağıdaki topolojik uzayları inceleyelim:

• \( X = (a, b) \) ve topolojisi \( T_X = \{\emptyset, \{a\}, \{b\}, X\} \).
• \( Y = (1, 2) \) ve topolojisi \( T_Y = \{\emptyset, Y\} \).

\( f: X \to Y \) fonksiyonunu \( f(a) = 1 \) ve \( f(b) = 2 \) olacak şekilde tanımlayalım.

\( f \) açıkça biyektiftir; \( X \)’teki her eleman \( Y \)’de tam olarak bir elemana karşılık gelir ve eşleme tersine çevrilebilir.

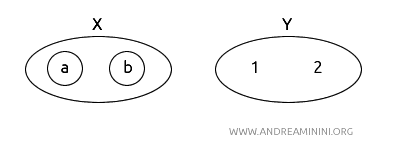
Not: Diyagramda açık kümeler dairelerle gösterilmiştir. \( X \)’te \{a\}, \{b\} ve \{a, b\} kümeleri açıktır; \( Y \)’de yalnızca \{1, 2\} açıktır. Boş kümeler tanımı gereği her zaman açık olduğundan, sadeleştirme amacıyla gösterilmemiştir.

Şimdi \( f \)’nin ve tersinin \( f^{-1} \)’in sürekliliğini ayrı ayrı inceleyelim.

• \( f \)’nin sürekliliği
  \( f \)’nin sürekli olabilmesi için, \( Y \)’deki her açık kümenin ön görüntüsü \( X \)’te açık olmalıdır. \( T_Y = \{\emptyset, Y\} \) olduğuna göre:
  • \( f^{-1}(\emptyset) = \emptyset \) → \( T_X \)’te açıktır,
  • \( f^{-1}(Y) = X \) → \( T_X \)’te açıktır.
  Dolayısıyla \( f \) sürekildir.
• \( f^{-1} \)’in sürekliliği
  Ters fonksiyon \( f^{-1}: Y \to X \)’te \( f^{-1}(1) = a \), \( f^{-1}(2) = b \) olsun. \( X \)’teki açık kümelerin ön görüntülerini inceleyelim:
  • \( f^{-1}(\emptyset) = \emptyset \) → \( T_Y \)’de açıktır,
  • \( f^{-1}(\{a\}) = \{1\} \) → \( T_Y \)’de açık değildir,
  • \( f^{-1}(\{b\}) = \{2\} \) → \( T_Y \)’de açık değildir,
  • \( f^{-1}(X) = Y \) → \( T_Y \)’de açıktır.
  Bazı ön görüntüler açık olmadığından, \( f^{-1} \) sürekli değildir.

Sonuç olarak, \( f \) biyektif ve sürekli olmasına karşın tersinin sürekliliği sağlanmadığı için \( f \) bir homeomorfizma değildir.

Bu örnek, bir fonksiyonun sürekli ve biyektif olmasının, tersinin de sürekli olacağını garanti etmediğini açıkça gösterir.

Not: \( f^{-1} \)’in sürekli olmamasının nedeni, topolojilerin “incelik” düzeylerinin farklı olmasıdır: \( X \)’in topolojisi daha ayrıntılı, \( Y \)’ninki ise daha kabadır (yalnızca \( \emptyset \) ve \( Y \) kümelerini içerir).

Örnek 2

Şimdi farklı topolojiler altında ikinci bir örneği inceleyelim:

• \( X = (a, b) \) ve \( T_X = \{\emptyset, \{a\}, X\} \).
• \( Y = (1, 2) \) ve \( T_Y = \{\emptyset, \{1\}, Y\} \).

\( f: X \to Y \) fonksiyonunu \( f(a) = 1 \), \( f(b) = 2 \) olarak tanımlayalım.

\( f \) yine biyektiftir.

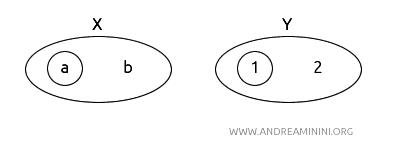
Şimdi \( f \) ve \( f^{-1} \)’in sürekliliğini inceleyelim.

• \( f \)’nin sürekliliği
  \( Y \)’deki açık kümeler \( \emptyset \), \(\{1\}\) ve \( Y \)’dir:
  • \( f^{-1}(\emptyset) = \emptyset \) → \( T_X \)’te açıktır,
  • \( f^{-1}(\{1\}) = \{a\} \) → \( T_X \)’te açıktır,
  • \( f^{-1}(Y) = X \) → \( T_X \)’te açıktır.
  Tüm ön görüntüler açık olduğundan \( f \) sürekildir.
• \( f^{-1} \)’in sürekliliği
  \( X \)’teki açık kümeler \( \emptyset \), \(\{a\}\) ve \( X \)’tir:
  • \( f^{-1}(\emptyset) = \emptyset \) → \( T_Y \)’de açıktır,
  • \( f^{-1}(\{a\}) = \{1\} \) → \( T_Y \)’de açıktır,
  • \( f^{-1}(X) = Y \) → \( T_Y \)’de açıktır.
  Bu durumda \( f^{-1} \) de süreklidir.

Dolayısıyla \( f \) biyektif, sürekli ve tersi de sürekli olduğundan, \( f \) bir homeomorfizmadır.

Önceki örnekle arasındaki fark, burada kullanılan topolojilerin birbiriyle daha uyumlu olmasıdır.

Not: Bu örnek, \( X \) ve \( Y \) üzerindeki topolojiler uygun şekilde seçildiğinde, ters fonksiyonun sürekliliğinin - dolayısıyla bir homeomorfizmanın - sağlanabileceğini göstermektedir.

Homeomorfizmalar ile diğer topolojik dönüşümler arasındaki fark

“Homeomorfizma” terimi kimi zaman topolojik dönüşümlerle eş anlamlıymış gibi kullanılsa da, gerçekte bu dönüşümlerin özel bir alt sınıfını ifade eder.

Homeomorfizmalar ile genel topolojik dönüşümler birbiriyle yakından ilişkili olmakla birlikte aynı kavram değildir:

• Topolojik dönüşümler
  Süreklilik ve bağlantılılık gibi temel özellikleri koruyan her türlü dönüşümü kapsayan geniş bir sınıftır. Bu sınıfa homeomorfizmalar dâhil olduğu gibi, izotopi, homotopi ve difeomorfizma gibi diğer dönüşümler de girer.
• Homeomorfizmalar
  Hem biyektif hem de sürekli olup tersleri de sürekli olan dönüşümlerdir. İki uzay arasında geri çevrilebilir bir eşleme kurar ve uzayların topolojik yapısını bütünüyle korur. Homeomorfizma ile ilişkilendirilen iki uzay, geometrik olarak farklı görünseler bile topolojik olarak ayırt edilemez.

Özetle, her homeomorfizma bir topolojik dönüşümdür; ancak her topolojik dönüşüm homeomorfizma değildir.

Bazı dönüşümler topolojik özellikleri korusa da, belirli ek koşulları sağlamadıkları için sıkı anlamda homeomorfizma sayılmaz.

Tamamlayıcı notlar

Aşağıda homeomorfizmalarla ilgili bazı ek gözlemler yer almaktadır:

• Topolojik özellik
  Topolojik özellik, bir uzayın homeomorfizma altında değişmeden kalan içsel bir niteliğidir. Yani iki uzay homeomorfikse (aralarında sürekli, biyektif ve tersine de sürekli bir eşleme varsa) aynı topolojik özelliklere sahiptirler.
• Homeomorfizmalar üzerine Hausdorff teoremi
  Bu teoreme göre, \( f: X \to Y \) bir homeomorfizma ve \( X \) bir Hausdorff uzayıysa, \( Y \) de Hausdorff’tur. Başka bir ifadeyle, homeomorfizmalar topolojik özellikleri koruduğundan, Hausdorff uzaylardaki nokta ayrımı özelliği \( X \)’ten \( Y \)’ye aktarılır.
• Homeomorfizma kavramının soyut cebirdeki karşılığı grup izomorfizmasıdır. İzomorfizma cebirsel yapıyı (işlemleri) korurken, homeomorfizma topolojik yapıyı, yani açık kümelerin örgüsünü korur.

Ve benzeri biçimde devam eder.