Topolojik Uzaylarda Düzenlilik
Bir topolojik uzay \( X \), aşağıdaki iki koşulu sağlıyorsa düzenli (regular) olarak adlandırılır:
- Tek noktalı kümeler kapalıdır. Başka bir deyişle, \( X \)'teki her nokta kendi başına kapalı bir kümedir.
- Noktalar ile kapalı kümeler ayrılabilir. Eğer \( a \in X \) bir nokta ve \( a \)'yı içermeyen bir kapalı küme \( C \subset X \) varsa, kesişmeyen iki açık küme \( U \) ve \( V \) bulunur; öyle ki \[ a \in U, \quad C \subset V, \quad U \cap V = \emptyset \]
Düzenlilik, topolojide bir ayrım özelliğidir. Hausdorff uzaylara göre daha güçlü bir koşul getirir, çünkü yalnızca noktaları değil, noktalarla kapalı kümeleri de ayırabilmeyi gerektirir.
Ayrıca, bir uzay hem düzenli hem de sayılabilir bir tabana sahipse, Urysohn teoremine göre metrikleştirilebilir. Yani bu tür uzaylara uygun bir metrik tanımlanabilir.
Hausdorff Uzaylarla Karşılaştırma
Hausdorff uzaylarda yalnızca iki farklı noktanın kesişmeyen açık kümelerle ayrılması gerekir. Düzenli uzaylarda ise bir nokta ile onu içermeyen kapalı bir kümenin ayrılması şarttır. Bu nedenle düzenlilik, Hausdorff koşulundan daha güçlü bir özelliktir.
Not. Her düzenli uzay normal değildir, ancak her normal uzay düzenlidir. Normal bir uzayda, kesişmeyen iki kapalı küme de kesişmeyen açık kümelerle ayrılabilir. Bu, düzenliliğin bir genellemesidir.
Unutulmamalıdır ki düzenlilik, ayrım aksiyomlarından sadece biridir. Bir uzay düzenli olabilir ama Hausdorff olmayabilir; ya da tersi geçerli olabilir. Topolojide bu tür örnekler oldukça yaygındır.
Bir Örnek: Gerçek Sayılar Doğrusu
Düzenli uzaylara en bilinen örnek, standart topolojiye sahip gerçek sayılar doğrusu \( \mathbb{R} \)'dir.
\( x = 2 \) noktasını ve onu içermeyen kapalı küme \( C = (-\infty, 0] \cup [5, \infty) \)'yi düşünelim.
Burada \( C \) kapalıdır ve \( x = 2 \) bu kümenin dışındadır.
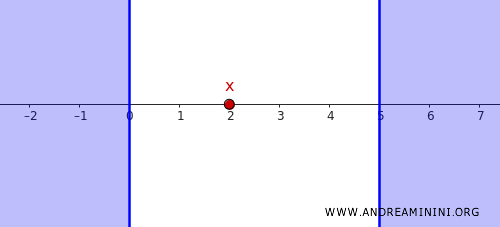
Amacımız \( x \)'i \( C \)'den ayıran açık kümeleri bulmaktır. \( C \)'nin tümleyeni zaten açık olduğundan, \( x \)'i içine alan bir açık aralık seçebiliriz. Örneğin:
\[ (a, b) = (0, 5) \]
Şimdi \( x = 2 \)'yi içine alan daha dar bir aralık seçelim:
\[ 0 < c < 2 < d < 5 \]
örneğin \( c = 1 \) ve \( d = 3 \).
Buna göre iki açık küme tanımlayabiliriz:
- \( U = (1,3) \), bu küme \( x = 2 \)'yi içerir.
- \( V = (-\infty,1) \cup (3,\infty) \), bu küme \( C \)'nin tamamını kapsar.
Bu iki açık küme kesişmez, yani \( U \cap V = \emptyset \). Dolayısıyla düzenlilik koşulu sağlanmıştır.
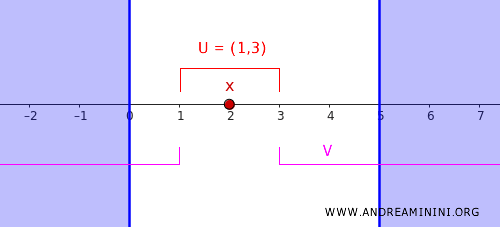
Sonuç olarak, gerçek sayılar doğrusunda bir noktayı ve onu içermeyen kapalı bir kümeyi, kesişmeyen iki açık küme yardımıyla ayırabildik. Bu, \( \mathbb{R} \)'nin standart topolojide düzenli bir uzay olduğunu açıkça gösterir.
Ek Açıklamalar
Düzenlilik kavramı, topolojideki ayrım aksiyomları (separation axioms) arasında önemli bir yere sahiptir. Bu aksiyomlar, bir uzayın elemanlarını açık kümeler aracılığıyla ne kadar hassas bir şekilde ayırt edebildiğini gösterir.
Not. Basitçe söylersek, bir uzay Hausdorff ise iki farklı nokta kesişmeyen açık kümelerle ayrılabilir. Bir uzay düzenli ise, bir nokta ile onu içermeyen kapalı bir küme aynı şekilde ayrılabilir. Bu özellikler, topolojinin "ayırma gücünü" - yani uzayların yapısal çözünürlüğünü - anlamamızda kilit rol oynar.
Düzenlilik, topolojik yapıların daha derin özelliklerini incelemek için temel bir adımdır ve metrikleştirilebilir uzayların tanımlanmasında merkezi bir kavramdır.