Ne açık ne de kapalı kümeler

Topolojide bazı kümeler vardır ki, ne açık ne de kapalıdır. Yani bu kümeler, iki türün de tanımına uymadıkları için arada kalmış gibidir.

Bu durum genellikle, bir kümenin açık kümeler arasında tanımlanmadığı veya herhangi bir açık kümenin tümleyeniyle örtüşmediği topolojilerde ortaya çıkar.

Dolayısıyla, böyle bir küme aynı zamanda bir kapalı küme olarak da kabul edilemez.

Not: Gerçek sayılar üzerindeki klasik topolojide, ne açık ne de kapalı kümeleri hayal etmek genellikle kolay değildir. Fakat topolojinin daha genel yapılarında bu tür kümelerin bulunması tamamen doğaldır. Aşağıdaki örnek, konuyu çok daha net hale getirecektir.

Somut Bir Örnek

Diyelim ki elimizde \( X = \{a,b,c,d\} \) kümesi var ve bu küme üzerinde şu açık kümeleri içeren bir topoloji \( T \) tanımlı:

\( \{b\} \), \( \{a,b\} \), \( \{c,d\} \), \( \{b,c,d\} \), \( \{a,b,c,d\} \) ve boş küme (Ø).

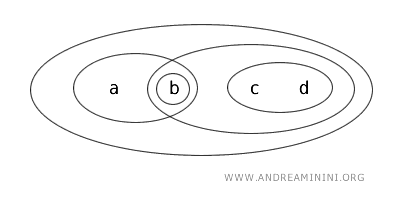
Şimdi \( X \) kümesinin \( \{b,c\} \) altkümesini inceleyelim.

• \( \{b,c\} \) açık kümeler listesinde yer almadığı için açık değildir.
• Ayrıca, \( \{b,c\} \) kapalı da değildir; çünkü tümleyeni \( X \setminus \{b,c\} = \{a,d\} \), açık kümeler arasında bulunmaz.

Yani, bu topoloji içinde \( \{b,c\} \) ne açık ne de kapalıdır.

Böyle örnekler, topolojinin farklı yapılarını anlamak için oldukça faydalıdır. Bu sayede, "açık" ve "kapalı" kavramlarının aslında mutlak değil, tanımlanan topolojiye göre değişen kavramlar olduğunu fark ederiz.