Hausdorff Uzayı Nedir?
Hausdorff uzayı, topolojide çok önemli bir kavramdır. Bu tür uzaylarda, birbirinden farklı iki nokta her zaman ayrık açık komşuluklarla birbirinden ayrılabilir. Bu, her noktanın diğerlerinden kesin olarak ayırt edilebildiği anlamına gelir.
Daha basit bir şekilde söylersek, bir Hausdorff uzayında herhangi iki nokta \( x \) ve \( y \) için kesişmeyen açık kümeler \( U \) ve \( V \) bulunabilir, yani \( U \cap V = \emptyset \).
Bu özellik, Öklid uzayında sezgisel olarak algıladığımız uzaklık ve ayrılık fikrinin topolojik bir karşılığıdır.
Hausdorff uzayları, dizilerin ve limit kavramının açık biçimde tanımlanabilmesi nedeniyle analiz, geometri ve topoloji alanlarında büyük önem taşır.
Ayrıca, bu tür uzaylarda tekil noktalar kapalı kümelerdir. Yani, bir noktanın dışındaki tüm noktaların oluşturduğu küme her zaman açık olur.
Örneklerle Anlayalım
Örnek 1: Gerçek Sayılar Doğrusu
Gerçek sayılar kümesi \(\mathbb{R}\) üzerinde tanımlı standart topolojiyi ele alalım.

Bu topolojide tekil noktalar açık değildir. Çünkü açık bir küme, içindeki her noktanın etrafında küçük bir aralık içermelidir. Ancak iki gerçek sayı arasında sonsuz sayı bulunduğundan, \( \{x\} \) gibi tekil noktalar bu koşulu sağlamaz.
Açıklama: Açık bir küme, her noktası için o noktayı tamamen içeren bir aralık bulundurmalıdır. Tek bir nokta, etrafında bu tür bir aralık oluşturamaz. Bu nedenle tekil noktalar açık değildir.
Buna karşın, her noktanın dışındaki tüm noktaların oluşturduğu \( \mathbb{R} \setminus \{x\} \) kümesi açıktır.

Dolayısıyla, tekil noktalar kapalı kümelerdir çünkü tümleyenleri açıktır.
Gerçek sayılar doğrusu aynı zamanda bir Hausdorff uzayıdır. Herhangi iki farklı nokta \( a \) ve \( b \) için, kesişmeyen açık aralıklar seçmek mümkündür.
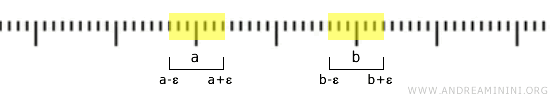
Örneğin, \( a < b \) ise, \( (a-\epsilon, a+\epsilon) \) ve \( (b-\epsilon, b+\epsilon) \) aralıklarını alabiliriz. \( \epsilon \) yeterince küçük seçilirse bu aralıklar kesişmez.
Bu durum, standart topolojinin Hausdorff özelliğine sahip olduğunu gösterir.
Örnek 2: Ayrık Topoloji
Şimdi X = {1,2,3} kümesi üzerinde tanımlı ayrık topolojiyi inceleyelim.
Bu topolojide her bir nokta kendi başına bir açık kümedir. Yani X'in tüm alt kümeleri açıktır:
- Boş küme \( \emptyset \)
- Tek noktalı kümeler \( \{1\} \), \( \{2\} \), \( \{3\} \)
- İki elemanlı kümeler \( \{1, 2\} \), \( \{1, 3\} \), \( \{2, 3\} \)
- Tüm küme \( \{1, 2, 3\} \)
Toplamda \( 2^3 = 8 \) açık küme vardır. Yani X'in bütün alt kümeleri açık kümelerdir.
Ayrık topolojiye sahip bir uzay her zaman Hausdorff uzayıdır.
Tanım gereği, farklı iki nokta \( x \) ve \( y \) için kesişmeyen açık komşuluklar \( U \) ve \( V \) bulunabiliyorsa uzay Hausdorff'tur.
Burada, X = {1,2,3} kümesinden seçilen herhangi iki farklı nokta için \( U = \{x\} \) ve \( V = \{y\} \) kümeleri bu koşulu sağlar. Bu iki kümenin kesişimi boştur: \( U \cap V = \emptyset \).
Örneğin, x={1} ve y={2} seçilirse, \( \{1\} \cap \{2\} = \emptyset \).
Dolayısıyla, iki nokta ayrık açık kümelere sahiptir. Aynı durum diğer tüm nokta çiftleri için de geçerlidir.
Ayrık topolojide tekil noktalar açık mı kapalı mı? Bu soru ilk bakışta kafa karıştırıcı olabilir. Ayrık topoloji bir Hausdorff uzayıysa, tekil noktalar kapalı olmalıdır. Ancak tanım gereği bunlar zaten açıktır. Peki bu nasıl mümkündür?
Aslında, topolojide bir küme hem açık hem de kapalı olabilir. Bu tür kümelere açık-kapalı kümeler (clopen set) denir. Topolojide "kapalı" kavramı, "açığın tersi" anlamına gelmez.
Ayrık topolojide her tekil nokta {x} aynı zamanda kapalıdır çünkü onun tümleyeni, yani x dışındaki tüm noktaların birleşimi, bir açık kümedir.
Dolayısıyla, bir tekil noktanın tümleyeni açık olduğunda, o nokta da bir kapalı kümedir.
Örneğin, X={1,2,3} kümesinde {1} elemanı açık bir kümedir. Aynı zamanda kapalıdır çünkü tümleyeni X/{1}={2,3} açık bir kümedir. Açık bir kümenin tümleyeni her zaman kapalıdır.
Sonuç olarak, ayrık topolojide her tekil nokta hem açık hem de kapalıdır. Çünkü tüm alt kümeler açık, tümleyenleri de açık olduğundan kapalıdır.
- Açık: Ayrık topolojide her nokta doğası gereği açık bir kümedir.
- Kapalı: Tümleyeni X/{x}, yani {x} dışındaki tüm elemanlardan oluşan küme, açık kümelerin birleşimidir. Bu da {x} kümesini kapalı yapar.
Ayrık topoloji ile standart topoloji arasındaki temel fark, standart topolojide her alt kümenin açık olmamasıdır. Yalnızca her noktası için bir açık komşuluk içeren kümeler açık kabul edilir.
Hausdorff Uzayının Önemi
Hausdorff uzayları, topolojide limit ve süreklilik kavramlarının doğru tanımlanabilmesini sağlar. Bu tür uzaylarda yakınsayan bir dizi her zaman tek bir limite sahip olur.
- Tekil limit özelliği: Hausdorff uzayı X'te yakınsayan her dizi yalnızca X'in bir noktasına yakınsar. Eğer bir dizi iki farklı noktaya yakınsıyor olsaydı, bu noktaların açık komşulukları mutlaka kesişirdi ve Hausdorff koşulu bozulurdu.
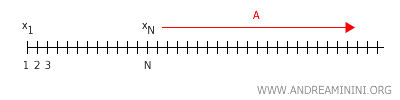
İspat: Hausdorff bir uzay X (örneğin, gerçek sayı doğrusu X=ℝ) düşünelim. Diyelim ki bir dizi x1, x2, x3,... hem x'e hem y'ye yakınsıyor. Bir topolojik uzayda dizi yakınsaması tanımına göre, yeterince büyük n değerleri için xn noktaları x'in bir A komşuluğu içinde olmalıdır.
Aynı şekilde, başka bir tamsayı M için xn noktaları y'nin bir B komşuluğu içinde olmalıdır.
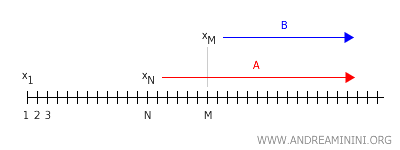
Eğer bu iki komşuluk kesişiyorsa, \( A \cap B \neq \emptyset \) olur ve Hausdorff koşulu ihlal edilir. Dolayısıyla bir dizi aynı anda iki farklı noktaya yakınsayamaz. Sonuç olarak, Hausdorff uzayında her dizi yalnızca tek bir noktaya yakınsar.
Bu özellik sayesinde Hausdorff uzayları, matematiğin hem teorik hem de uygulamalı alanlarında düzenli ve sezgisel bir yapı sağlar.