Açık Kümelerin Topolojisi
Bir küme X üzerinde tanımlanan topoloji T, X’in “açık” olarak kabul edilen alt kümelerinden oluşan bir koleksiyondur ve aşağıdaki koşulları sağlar:
- Boş küme Ø ve X kümesinin kendisi tanım gereği açıktır.
- Herhangi bir sonlu sayıda açık kümenin birleşimi ve kesişimi yine açık kümedir.
Başka bir ifadeyle, T koleksiyonu yalnızca X’in “açık” kabul edilen alt kümelerini içerir ve birleşim ile kesişim işlemleri altında kapalıdır.
Kümeler koleksiyonu, elemanları başka kümeler veya alt kümeler olan bir kümedir.
Bu durumda X kümesi ile T topolojisi birlikte bir topolojik uzay oluşturur ve genellikle (X,T) çiftiyle gösterilir.
Not: Basitleştirme amacıyla genellikle “X bir topolojik uzaydır” denir. Ancak hatırlanmalıdır ki bir topolojik uzay iki bileşenden oluşur: topoloji T (alt kümeler koleksiyonu) ve kümenin kendisi X.
Boş küme neden her zaman açık kabul edilir?
Boş küme, her topolojik uzayda tanım gereği açık kabul edilir.
Bu kural, topoloji tanımının temel bir parçasıdır ve topolojik aksiyomların tutarlılığını ve bütünlüğünü sağlar.
Uygulamalı bir örnek
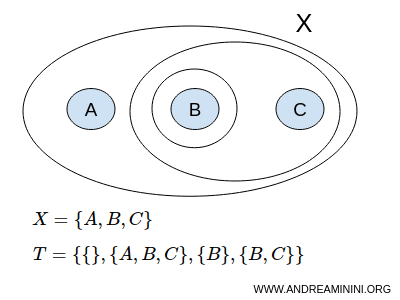
Üç elemandan oluşan bir X kümesini ele alalım: A, B ve C.
$$ X = \{ A,B,C \} $$
Bir topoloji T aşağıdaki alt kümelerden oluşabilir: { }, {A,B,C}, {B}, {B,C}.
$$ T = \{ \{ \},\{A,B,C \}, \{ B \}, \{ B,C \} \} $$
Burada { } boş küme Ø’yi, {A,B,C} ise tüm küme X’i temsil eder; yani bunlar X’in doğrudan (improper) alt kümeleridir.
Tanım gereği hem boş küme hem de tüm küme X açık kabul edilir.
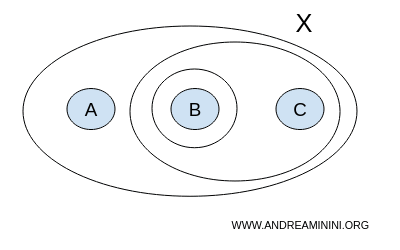
Bir topoloji, açık kümelerden oluşur ve tanım gereği bu kümelerin birleşimi ve kesişimi de yine açık küme verir.
Bu örnekte, T’de yer alan alt kümelerin birleşimleri yine T’nin elemanları olduğundan, birleşim işlemi altında kapalıdır.
$$ \{ B \} \cup \{ B, C \} \subseteq \{ B, C \} \subseteq T$$
$$ \{ B \} \cup \{ A, B, C \} \subseteq \{ A, B, C \} \subseteq T$$
$$ \{ B \} \cup \{ \} \subseteq \{ B \} \subseteq T $$
$$ \{ B \} \cup \{ B \} \subseteq \{ B \} \subseteq T$$
Aynı şekilde, T’deki alt kümelerin kesişimleri de yine T’nin bir elemanıdır; dolayısıyla kesişim işlemi altında da kapalıdır.
$$ \{ B \} \cap \{ B, C \} \subseteq \{ B \} \subseteq T$$
$$ \{ B \} \cap \{ A, B, C \} \subseteq \{ B \} \subseteq T$$
$$ \{ B \} \cap \{ \} \subseteq \{ \} \subseteq T $$
$$ \{ B \} \cap \{ B \} \subseteq \{ B \} \subseteq T$$
Dolayısıyla T koleksiyonu, X kümesi üzerinde bir topoloji oluşturur çünkü gerekli tüm koşulları sağlamaktadır.
Örnek 2
Şimdi önceki örnekten biraz farklı bir koleksiyona bakalım.
X kümesi yine aynı kalsın.
$$ X = \{ A,B,C \} $$
Bu kez T koleksiyonu {A} alt kümesini de içersin: { }, {A,B,C}, {A}, {B}, {B,C}.
$$ T = \{ \{ \},\{A,B,C \}, \{ A \}, \{ B \}, \{ B,C \} \} $$
Bu yeni T koleksiyonu bir topoloji oluşturmaz çünkü topoloji tanımındaki koşullardan en az birini sağlamaz.
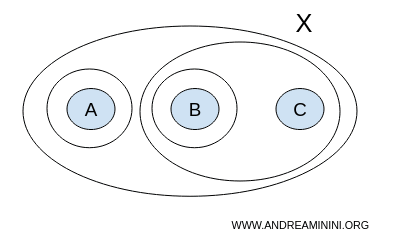
Örneğin, {A} ve {B} kümelerinin birleşimi {A,B} kümesini verir, ancak bu küme T koleksiyonunda yer almaz.
$$\require{cancel} \{ A \} \cup \{ B \} = \{ A, B \} \cancel{\notin} T $$
Dolayısıyla {A} ve {B} kümeleri T içinde oldukları için “açık” kabul edilse de, birleşimleri olan {A,B} kümesi T’nin dışında kaldığından açık değildir.
$$ T = \{ \{ \},\{A,B,C \}, \{ A \}, \{ B \}, \{ B,C \} \} $$
Bu durum, bir koleksiyonun açık kümelerin topolojisi olarak kabul edilebilmesi için gerekli temel koşullardan birinin ihlal edildiğini gösterir.
Sonuç olarak, T koleksiyonu X kümesinin bir topolojisi değildir.
Ve örnekler bu şekilde sürdürülebilir.