Açık Küre Nedir?

Topolojide açık küre, bir noktadan (merkez c) belirli bir uzaklıktaki tüm noktaların oluşturduğu kümedir. Bu uzaklığa yarıçap (r) denir. Başka bir deyişle, açık küre; merkezine olan uzaklığı r'den küçük olan tüm noktaları içerir. $$ B(c, r) = \{ x \in M \mid d(c, x) < r \} $$

Açık küre kavramı, \( M \) ile gösterilen bir metrik uzayda tanımlanır. Burada \( d \), uzaydaki iki nokta arasındaki mesafeyi ölçen bir metriktir, yani bir "uzaklık ölçüsü"dür.

Bir açık küre, yalnızca merkezi ve yarıçapıyla tanımlanır. Ancak "açık" olmasının nedeni, her açık küre içinde, tamamen onun içinde kalan daha küçük bir açık küre bulunabilmesidir. Bu özellik, topolojik yapıların temel taşlarından biridir.

Not: Açık küreler, ölçekleme ve öteleme işlemlerinden etkilenmez. Yani, boyutlarını ya da konumlarını değiştirseniz bile, açık küre olma özelliği değişmez.

R² düzlemini düşünelim. Burada, bir p=(x,y) noktası ile merkez c=(x₀,y₀) arasındaki mesafe Öklid metriğiyle ölçülür:

$$ d(p,c) = \sqrt{(x-x_0)^2+(y-y_0)^2} $$

Açık dairesel komşuluklar, düzlemin topolojik yapısını tanımlamada temel bir rol oynar. Topolojinin inşasında bu kavram, yapı taşlarından biri olarak kabul edilir.

R² düzleminin standart topolojisi, açık kürelerin oluşturduğu bir sistem üzerine kuruludur.

$$ B = \{ B(p, r) \ | \ p \in R^2, \ r > 0 \} $$

Burada p, iki boyutlu uzaydaki bir noktayı p=(x,y) olarak gösterir; r ise bu nokta etrafındaki komşuluğun yarıçapıdır.

Bu, düzlem için tanımlanabilecek tek topoloji değildir; ancak en sık kullanılan ve en doğal olanıdır. Matematikteki pek çok topolojik kavram, bu temel yapı üzerine kuruludur.

Bir açık küredeki her $ q \in B(p,r) $ noktası, aynı zamanda B(q,ε) biçiminde, tamamen B(p,r)'nin içinde kalan daha küçük bir açık kürenin merkezidir.

$$ \forall \ q \in B(p,r) \ \exists \ \epsilon > 0 \ \text{öyle ki} \ B(q,ε) \subset B(p,r) $$

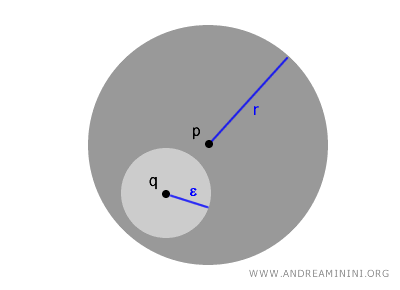
Bu özellik, açık kürelerin topolojik sistemlerde neden bu kadar önemli olduğunu gösterir: her nokta, kendi içinde başka bir "küçük açık küreye" ev sahipliği yapar.

\(\mathbb{Z}\)'nin \(\mathbb{R}\)'nin standart topolojisinden miras aldığı topoloji, \(\mathbb{Z}\) üzerindeki ayrık topolojiyle birebir aynıdır.