Altuzay Topolojisi

Bir topolojik uzay \( (X, T) \) verildiğinde, burada \( X \) bir küme, \( T \) ise \( X \) üzerindeki topolojiyi tanımlayan açık kümeler ailesidir. Eğer \( Y \), \( X \)’in bir altkümesiyse, \( Y \) üzerindeki altuzay topolojisi şu şekilde tanımlanır:
\[ T_Y = \{ U \cap Y \mid U \in T \} \] Yani, \( Y \)’deki her açık küme, \( X \)’teki bir açık kümenin \( Y \) ile kesişimi biçiminde elde edilir. Bu topolojiye türetilmiş topoloji de denir.

Başka bir deyişle, \( V \subseteq Y \) olan bir küme, yalnızca \( Y \) ile \( X \)’teki bir açık kümenin kesişimi şeklinde yazılabiliyorsa, altuzay topolojisinde açık kabul edilir.

Dolayısıyla altuzay topolojisindeki bütün açık kümeler \( U \cap Y \) biçimindedir; burada \( U \), \( X \)’te açık bir kümedir.

$$ V_{Y'de\ açık} = U \cap Y $$

Benzer biçimde, altuzay topolojisindeki tüm kapalı kümeler \( C \cap Y \) biçimindedir; burada \( C \), \( X \)’te kapalı bir kümedir.

$$ V_{Y'de\ kapalı} = C \cap Y $$

Böylece, bir topolojik altuzay, bir topolojik uzayın altkümesidir ve topolojisini orijinal uzaydan miras alır.

Not. Altuzay topolojisinde açık olan bir küme, genel topolojik uzay $ X $’te açık olmak zorunda değildir. Bazı kümeler $ Y $’de açık olup $ X $’te kapalı olabilir veya tam tersi de mümkündür. Ayrıca, hem $ Y $ hem de $ X $’te açık veya kapalı olan kümeler de bulunur. Bunun yanında, hem açık hem kapalı olan “clopen” kümeler de vardır. Bu notların ilk örneğinde bu durumu gösterip nedenini açıklıyorum.

Uygulamalı Örnek

Açık kümeleri açık aralıklar olan standart topolojiye sahip \( \mathbb{R} \) uzayını ele alalım.

\( Y = [0, 1] \) kümesi \( \mathbb{R} \)’nin bir altkümesi olsun.

\( Y \) üzerindeki altuzay topolojisi şu biçimdeki kümeleri içerir:

$$ U \cap [0, 1] $$

Burada \( U \), \( \mathbb{R} \)’de açık bir kümedir.

Örneğin, (-1, 0.5) kümesi \( \mathbb{R} \)’de açıktır.

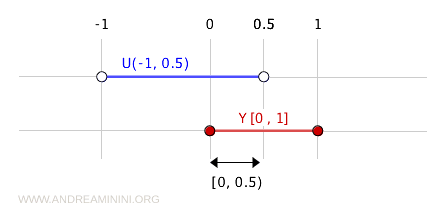
(-1, 0.5) kümesinin \( Y = [0, 1] \) ile kesişimi, \( Y \) üzerindeki altuzay topolojisinde açık bir kümedir:

$$ (-1, 0.5) \cap [0, 1] = [0, 0.5) $$

Dolayısıyla \( [0, 0.5) \) kümesi altuzay \( Y \)’de açıktır.

Öte yandan, $ [0, 0.5] $ kümesi altuzay topolojisinde kapalıdır çünkü $ X $’teki kapalı küme [-1, 0.5] ile $ Y $’nin kesişiminden elde edilir.

$$ [-1, 0.5] \cap [0, 1] = [0, 0.5] $$

Sonuç olarak, altuzay \( Y \), orijinal uzay \( X \)’ten topolojik yapısını devralır. Böylece, \( Y \)’deki açık kümeler, \( X \)’teki açık kümelerin \( Y \) ile kesişimidir.

Not. [0,a) veya (a,1] biçimindeki kümeler (0

Altuzay topolojisinde hem $ Y $ hem de $ X $’te açık olan kümeler vardır. Örneğin (0.2, 0.8) kümesi bunlardan biridir.

Aynı şekilde, hem $ Y $ hem de $ X $’te kapalı olan [0.2, 0.8] kümesi de buna örnektir.

Son olarak, \( Y = [0, 1] \) altuzayında \( [0, 1] \) kümesi hem açık hem de kapalıdır.

• Açık
  \( [0, 1] \) kümesinin altuzay \( Y \)’de açık olduğunu göstermek için, \( \mathbb{R} \)’de \( U \cap Y = [0, 1] \) olacak bir açık küme \( U \) bulmamız gerekir. \( U = \mathbb{R} \) seçersek, bu küme zaten \( \mathbb{R} \)’de açıktır. O hâlde: $$ U \cap Y = \mathbb{R} \cap [0, 1] = [0, 1] $$ Böylece \( [0, 1] \), altuzay \( Y \)’de açıktır.
• Kapalı
  \( [0, 1] \) kümesinin altuzay \( Y \)’de kapalı olduğunu göstermek için, \( \mathbb{R} \)’de \( C \cap Y = [0, 1] \) olacak bir kapalı küme \( C \) bulmamız yeterlidir. \( C = [0, 1] \) seçelim; bu küme \( \mathbb{R} \)’de kapalıdır. $$ C \cap Y = [0, 1] \cap [0, 1] = [0, 1] $$ O hâlde \( [0, 1] \), altuzay \( Y \)’de kapalıdır.

  Not: Alternatif olarak, \( [0, 1] \)’in \( Y \)’de kapalı olduğunu, \( Y \)’deki tümleyeni boş küme olduğu için de görebiliriz. Boş küme her topolojide açıktır. Açık bir kümenin tümleyeni kapalı olduğundan, \( [0, 1] \) kümesi \( Y \)’de kapalıdır.

Sonuç olarak, \( Y = [0, 1] \) altuzayında \( [0, 1] \) kümesi hem açık hem kapalıdır.

Bu tür kümelere İngilizcedeki “closed” ve “open” sözcüklerinin birleşiminden türetilen “clopen” adı verilir.

Örnek 2

Gerçel sayılar kümesi \(\mathbb{R}\) üzerindeki standart topolojiyi düşünelim.

Bu topolojide, $  a < b $ olmak koşuluyla her (a,b) aralığı açıktır.

\(\mathbb{R}\)’nin topolojik bir altuzayı, tamsayılar kümesi \(\mathbb{Z}\)’dir. Çünkü her tamsayı, gerçel sayılar kümesindeki uygun açık aralıkların kesişimiyle elde edilebilir.

Örneğin, 7 tamsayısı \(\mathbb{R}\)’deki açık küme (6.5,7.5) ile \(\mathbb{Z}\)’nin kesişiminden elde edilir:

$$ (6.5,7.5) \cap \mathbb{Z} = \{ 7 \} $$

Aynı yöntemle diğer tüm tamsayılar da elde edilebilir.

Dolayısıyla her tamsayı, \(\mathbb{Z}\)’nin topolojik altuzayında açık bir kümedir.

Benzer şekilde, \(\mathbb{Z}\)’nin her altkümesi de bu altuzayda açık bir kümedir.

Örneğin {6,7,8} kümesini elde etmek için (5.5,8.5) açık kümesini \(\mathbb{Z}\) ile kesiştirmek yeterlidir:

$$ (5.5,8.5) \cap \mathbb{Z} = \{ 6, 7, 8 \} $$

Bu \(\mathbb{Z}\) üzerindeki altuzay, aynı zamanda ayrık topoloji olarak adlandırılır.

Not: \(\mathbb{Z}\) üzerindeki ayrık topoloji, \(\mathbb{R}\)’deki standart topolojinin bir altuzayı değildir; kendi başına bağımsız bir topolojidir. Ancak \(\mathbb{Z}\)’nin, \(\mathbb{R}\)’deki standart topolojiden devraldığı altuzay topolojisi, \(\mathbb{Z}\) üzerindeki ayrık topolojiyle özdeştir.

Örnek 3

Standart topolojiye sahip üç boyutlu Öklid uzayı \(\mathbb{R}^3\)'ü ele alalım. Bu topolojide açık kümeler, açık topların birleşimleriyle tanımlanır.

Şimdi, orijinden uzaklığı 1 olan noktaların oluşturduğu birim küre \( S^2 \)'yi düşünelim:

$$ S^2 = \{ (x, y, z) \in \mathbb{R}^3 \mid x^2 + y^2 + z^2 = 1 \} $$

\( S^2 \) üzerindeki altuzay topolojisi şu şekilde tanımlanır:

$$ T_{S^2} = \{ U \cap S^2 \mid U \text{ } \mathbb{R}^3\text{'te açık bir kümedir} \} $$

Yani, \( V \subseteq S^2 \) olan bir küme, yalnızca \( S^2 \) ile \(\mathbb{R}^3\)'teki açık bir kümenin kesişimi biçiminde yazılabiliyorsa, altuzay topolojisinde açıktır.

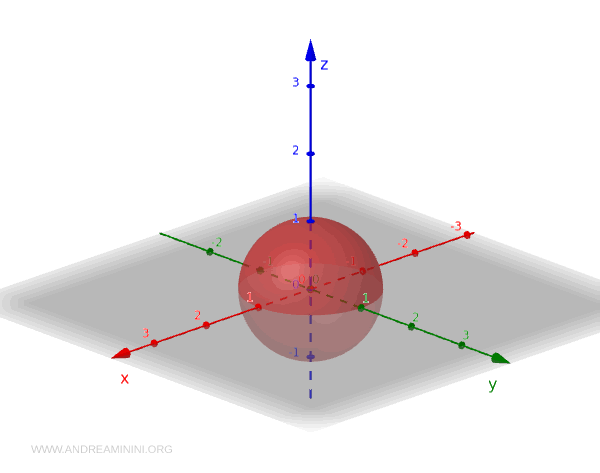
\( S^2 \) üzerindeki bazı açık küme örnekleri aşağıdadır:

• \(\mathbb{R}^3\)'teki açık kümelerin birleşimleri
  \( U = \{ (x, y, z) \in \mathbb{R}^3 \mid x^2 + y^2 + z^2 < 2 \} \) kümesini ele alalım. Bu kümenin \( S^2 \) ile kesişimi: $$ U \cap S^2 = S^2 $$ Çünkü \( S^2 \)'deki her nokta \( x^2 + y^2 + z^2 = 1 \) koşulunu sağlar ve bu değer 2'den küçüktür. Dolayısıyla \( S^2 \), kendi içinde açık bir kümedir.
• Kürenin bir bölümü
  \( U = \{ (x, y, z) \in \mathbb{R}^3 \mid x^2 + y^2 + z^2 = 1 \text{ ve } z > 0 \} \) kümesini ele alalım. Bu küme, birim kürenin üst yarım küresini temsil eder. Kesişim şu şekilde olur: $$ U \cap S^2 = \{ (x, y, z) \in S^2 \mid z > 0 \} $$ Bu küme, kürenin üst kısmını temsil eder ve altuzay topolojisi \( T_{S^2} \)'de açıktır.
• Açık kümeler ve kapanış
  Boş küme \( \emptyset \) ve tüm küre \( S^2 \) kendi üzerinde açıktır.
  • \( S^2 \)'deki açık kümelerin sonlu kesişimleri yine \( S^2 \)'de açıktır.
  • \( S^2 \)'deki açık kümelerin herhangi bir birleşimi de \( S^2 \)'de açıktır.

Sonuç olarak, \( S^2 \) küresi, \(\mathbb{R}^3\)'ün bir topolojik altuzayı olarak topolojik yapısını \(\mathbb{R}^3\)'ün standart topolojisinden devralır. \( S^2 \)'deki açık kümeler, \(\mathbb{R}^3\)'teki açık kümelerin \( S^2 \) ile kesişimlerinden oluşur.

Altuzay Topolojisinin Temel Özellikleri

Altuzay topolojisinin başlıca özellikleri şunlardır:

1. Açık kümeler
   \( Y \)'deki bütün açık kümeler \( U \cap Y \) biçimindedir; burada \( U \), \( X \)'te açık bir kümedir.
2. Boş küme ve tüm küme
   Boş küme \( \emptyset \) ve \( Y \)'nin kendisi her zaman \( Y \)'de açıktır:
   - \( \emptyset \) açıktır çünkü \( \emptyset = \emptyset \cap Y \).
   - \( Y \) açıktır çünkü \( Y = X \cap Y \).
3. Sonlu kesişimler
   \( Y \)'deki açık kümelerin sonlu sayıda kesişimi yine \( Y \)'de açıktır. Eğer \( V_1, \ldots, V_n \) açık kümelerse: $$ V_1 \cap \cdots \cap V_n = (U_1 \cap Y) \cap \cdots \cap (U_n \cap Y) = (U_1 \cap \cdots \cap U_n) \cap Y $$ Burada her \( U_i \), \( X \)'te açık bir kümedir ve \( X \)'teki açık kümelerin sonlu kesişimi de açıktır.
4. Keyfi birleşimler
   \( Y \)'deki açık kümelerin keyfi birleşimi yine \( Y \)'de açıktır. Eğer \( V_\alpha \), bir indeks kümesi \( I \)'deki her \( \alpha \) için \( Y \)'de açık ise: $$ \bigcup_{\alpha \in I} V_\alpha = \bigcup_{\alpha \in I} (U_\alpha \cap Y) = \left( \bigcup_{\alpha \in I} U_\alpha \right) \cap Y $$ Burada her \( U_\alpha \), \( X \)'te açık bir kümedir ve \( X \)'teki açık kümelerin birleşimi yine açıktır.

Ek Notlar

Altuzay topolojisiyle ilgili bazı ek bilgiler:

• \(\mathbb{R}^n\)'deki herhangi bir altküme \( Y \) üzerindeki standart topoloji, \(\mathbb{R}^n\)'ün altuzay topolojisiyle özdeştir.

  Örnek. \( Y=[-1,0)\cup(0,1] \) kümesini düşünelim. Bu küme \( \mathbb{R} \)'nin bir altkümestir. \( Y \) üzerindeki standart topolojide [-1,0) ve (0,1] aralıkları her ikisi de açıktır, çünkü bu aralıklar \( Y \)'nin \( \mathbb{R} \)'deki açık kümelerle kesişiminden elde edilir. Örneğin, \( \mathbb{R} \)'deki açık kümeler (-1.5,0.5) ve (0,1.5) olsun: $$ (-1.5,0.5) \cap Y = [-1,0) $$ $$ (0,1.5) \cap Y = (0,1] $$ Dolayısıyla \( Y \) üzerindeki standart topoloji, \( \mathbb{R} \)'deki standart topolojinin altuzay topolojisine denktir. Bu durumda [-1,0) ve (0,1] aralıkları \( Y \)'nin standart topolojisinde hem açık hem de kapalıdır (yani "clopen"). Çünkü [-1,0)'ın tümleyeni (0,1], (0,1]'in tümleyeni ise [-1,0)'dır.

• Altuzay Topolojisi Temel Teoremi
  Bu teorem şunu söyler: Bir topolojik uzay \(X\)'in topolojisi için bir temel $ B_X $ verilmişse ve \(Y \subset X\) bir altküme olarak alınırsa, \( B_X \)'teki kümelerin \( Y \) ile kesişimlerinden oluşan aile, \(Y\)'deki altuzay topolojisi için bir temel oluşturur: $$ B_Y = \{ B \cap Y \mid B \in B_X \} $$

Bu şekilde, altuzay topolojisinin yapısı ve özellikleri genel topolojik ilkelerden doğal olarak türetilmiş olur.